угол В равен 90 градусов,тк АВСД прямоугольник,следовательно угол ОВС равен 90-48=42 градуса. Треугольник АВО равен треугольнку СОД по двум сторонам и углу между ними,значит угол АВО равен углу ОСД и равен 48 градусам. НО тк угол С равен 90,то угол ВСО равен 90-48=42. Далее рассмотрим треугольник ВОС: в нём угол В равен углу С и равен 42 градусам. Тк. сумма углов треугольнка 189 градусов,то угол О-180-(угол В+уголС)=180-84=96. Угол ВОС и угол АОД вертикальные следовательно угол АОД равен 96 градусам
В сечении получаем пятиугольник, который для определения площади можно разделить на равнобедренные треугольник и трапецию. Основание РМ этой фигуры равно 6√2.
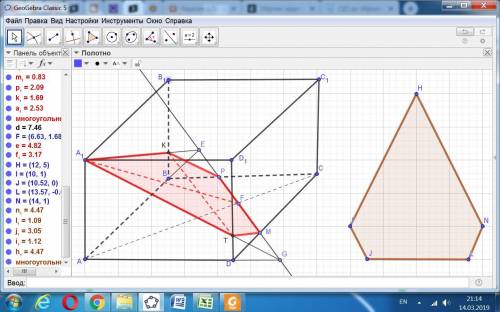
Заданная плоскость пересекает рёбра ВВ1 и ДД1 в точках К и Т, расстояние между которыми равно диагонали квадрата основания, то есть 8√2.
Отрезок А1F является суммой высот указанных фигур.
Отрезок СF равен как высота из прямого угла 6*6/(6√2) = 6/√2 = 3√2.
Отсюда находим А1F = √(4² + (8√2 - 3√2)²) = √(16 + 50) = √64 = 8.
Расстояние (из подобия) ДТ = (2*4/(8 + 2) = 8/10 = 4/5.
Высота трапеции равна ДТ/cos(A1FA) = (4/5)/(4/8) = 8/5.
Тогда высота треугольника равна 8 - (8/5) = 32/5.
Получаем ответ: S = (1/2)*(32/5)*8√2 + ((8√2 + 6√2)/2)*(8/5) =
= ((32/5)*4√2 + 56√2)/5 = (184√2)/5 кв.ед.
<ATM = 90°. Тогда треугольник ATM - прямоугольный.
По теореме Пифагора найдем ТМ (по условию ТМ - это диаметр окружности).
AM² = AT² + TM²
AM = AE+ME = 2+ 10 = 12.
TM² = AM² - AT² = 12² - 6² = 6²·2² - 6² = 6²·(4-1) = 3*6²,
TM = √(3*6²) = 6*√3.
Искомый радиус равен половине диаметра ТМ.
R = TM/2 = (6*√3)/2 = 3*√3.
Угол между касательной и секущей, проходящей через точку касания, равен половине отсекаемой дуги окружности.
<ATE = (1/2)*дуги_ТЕ,
Но также и вписанный <EMT = (1/2)*дуги_TE,
Тогда <ATE=<EMT=<AMT
Из прямоугольного треугольника ATM
sin(<AMT) = AT/AM = 6/12 = 1/2.
<AMT = arcsin(1/2) = 30° = <ATE.