Длина картона кратна и ширине, и длине карточки:
48:16=3, 48:12=4. Ширина картона НЕ кратна ни длине, ни ширине карточки.
По ширине нужно разметить первую линию разреза так, чтобы оставшаяся часть картона по ширине была кратна одному из размеров карточки.
Если отрезать первую полосу шириной 16 см, ширина оставшейся части картона будет 28 - не кратна ни одному размеру карточки.
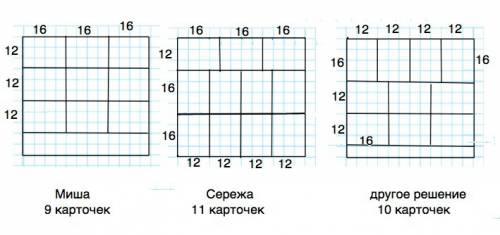
Следовательно, сначала нужно отрезать от картона полоску шириной в 12 см и разрезать на 3 части.
Оставшийся лист будет размером 32•48, и оба его размера теперь кратны длине карточки. Разрезав его по ширине на две полоски по 16 см, можно затем каждую разрезать на 4 карточки шириной 12 см, при этом излишков не образуется.
Если первую полоску отрезать шириной 16 см, ширина оставшейся части картона не будет кратной ни длине, ни ширине. Поэтому ее нельзя будет разрезать, чтобы не осталось лишнего картона.
Данный лист картона можно разрезать на 11 карточек, при этом не образуется излишков.
Если два треугольника имеют равный угол, то площади этих треугольников относятся как произведения сторон, заключающих этот угол.
Дано: ΔАВС, ΔА₁В₁С₁, ∠А = ∠А₁.
Доказать: Sabc /Sa₁b₁c₁ = (AB · AC) / (A₁B₁ · A₁C₁) .
Доказательство:
Наложим треугольники так, чтобы угол А совместился с углом А₁, а стороны А₁В₁ и А₁С₁ лежали на лучах АВ и АС соответственно.
Проведем ВН - высоту ΔАВС. ВН является так же и высотой треугольника А₁ВС₁.
Площади треугольников, имеющих общую высоту, относятся как их основания (стороны, к которым проведена высота):
Sabc / Sa₁bc₁ = AC / A₁C₁ (1)
Проведем С₁Н₁ - высоту ΔА₁В₁С₁. С₁Н₁ является так же и высотой треугольника АВС₁, значит
Sabc₁ / Sa₁b₁c₁ = AB / A₁B₁ (2)
Перемножим равенства (1) и (2):
(Sabc / Sa₁bc₁) · (Sabc₁ / Sa₁b₁c₁) = (AC / A₁C₁) · (AB / A₁B₁)
Так как Sa₁bc₁ и Sabc₁ это площадь одного и того же треугольника, она сокращается и получаем:
Sabc / Sa₁b₁c₁ = (AB · AC) / (A₁B₁ · A₁C₁)
5 долей - 15*5=75 градусов
3 доли - 15*3=45 градусов.