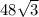
Объяснение:
Диагонали точкой пересечения делятся пополам в точке О.
Найдем координаты О по формулам середины отрезка:
А( 1 ; 0) ,С( -5 ;6). О-середина АС ,
х(О)= ( х(А)+х(С) ):2 у(О)= ( у(А)+у(С) ):2
х(О)=(1-5):2=-2 у(О)= (0+6):2=3
О(-2 ;3)
В( 1;2) ,О( -2 ;3). О-середина ВД , найдем координаты т Д.
х(О)= ( х(В)+х(Д) )/2 у(О)= ( у(В)+у(Д) )/2
2*х(О)= х(В)+х(Д) 2*у(О)= у(В)+у(Д)
х(Д) = 2*х(О)-х(В) у(Д) = 2*у(О)-у(В)
х(Д) = 2*(-2)-1 у(Д) = 2*3-2
х(Д) = -5 у(Д) = 4
Д(-5; 4)
ответ: Vmax≈78,6*π*√3 см³.
Объяснение:
Объём конуса V=1/3*π*R²*H, где R и H - радиус основания и высот конуса. По теореме Пифагора, R²+H²=L², где L - длина образующей конуса. Отсюда R²=L²-H² и тогда V(H)=1/3*π*H*(L²-H²)=1/3*π*(H*L²-H³). Находим производную V'(H)=1/3*π*(L²-3*H²) и приравниваем её к нулю. Отсюда следует уравнение L²=3*H², или H=L/√3. Если H<L/√3, то V'(H)>0, если H>L/√3, то V'(H)<0. Так как при переходе через точку H=L/√3 производная V'(H) меняет знак с + на -, то эта точка является точкой максимума функции V(H), и тогда наибольший объём конуса Vmax=1/3*π*(L³/√3-L³/[3*√3])=2*π*L³/(9*√3). И так как по условию L=10,2 см, то Vmax≈78,6*π*√3 см³.
Короткое решение:
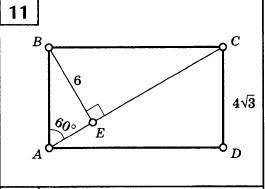
∠BCA = 30° ⇒ BE = BC/2 ⇒ BC = 12.
S(ABCD) = 4√3 * 12 = 48√3
Длинное решение:
Сначала найдем длину AE. Так как уже известна длина CD = AB, то по теореме Пифагора:
AE =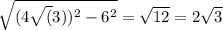
Теперь обозначим CE за x, а BC за y и составим два уравнения:
1)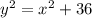
2)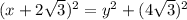 ⇔
⇔
Подставим из второго уравнения значение y^{2} в первое и решим:
ответ: