32,475 ед²
Объяснение:
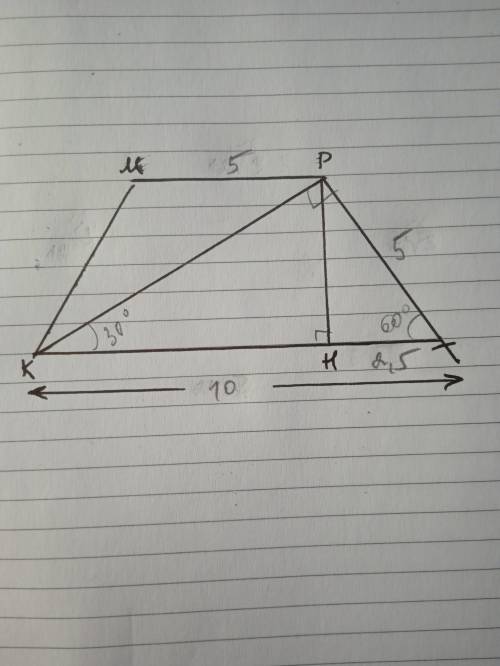
Дано: КМРТ - трапеция, КМ=РТ, КТ=10; ∠К=∠Т=60°. КР⊥РТ Найти S(КМРТ).
ΔКРТ - прямоугольный, ∠Т=60°, ∠РКТ=90-60=30°, т.к. сумма острых углов прямоугольного треугольника 90°
РТ=1\2 КТ=10:2=5 по свойству катета, лежащего против угла 30°
Проведем высоты МС и РН, рассмотрим ΔТРН - прямоугольный,
∠ТРН=90-60=30°, значит ТН=1/2 РТ=5:2=2,5.
По теореме Пифагора РН=√(РТ²-ТН²)=√(25-6,25)=√18,75≈4,33
ΔКМС=ΔТРН по катету и гипотенузе, значит КС=ТН=2,5;
МР=СН=10-2,5-2,5=5.
S=(МР+КТ):2*РН=(5+10):2*4,33≈32,475 ед²
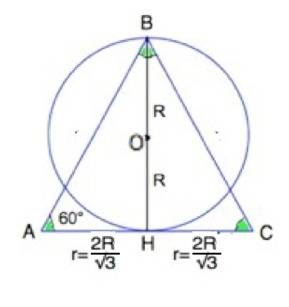
Сделаем схематический рисунок осевого сечения конуса и шара так, чтобы высота конуса наложилась на диаметр шара, при этом они совпадут ( равны по условию),
Осевое сечение шара - круг, конуса - треугольник, в данном случае - равносторонний треугольник, т.к. образующая составляет с плоскостью основания угол 60°.
Примем радиус шара равным R. Тогда высота конуса BH=2 R.
Высота ( она же медиана и биссектриса) делит равносторонний треугольник АВС на два равных прямоугольных с острыми углами ВАН=ВСН=60°.
Радиус основания конуса=АН=СН= ВН:tg60°=2R:√3
V (к)=πr•h:3=π(2R/√3)²•2R/3
V(к)=8πR³/9
V(ш)=4πR³:3
Искомое отношение V (кон):V(шара)
(8πR³/9):(4πR³:3)=(8πR³•3):(9•4πR³)=2:3
Получившийся 4-угольник - ромб, так как его стороны равны половине диагонали прям-ка.
Диагонали ромба равны сторонам прямоугольника, т.к. они взаимно перпендикулярны.
S = (1/2) d1*d2 = (1/2)a*b = (1/2)*36 = 18 cm^2
ответ: 18 см^2.