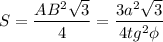
а) 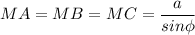
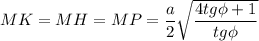
б) 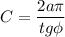
в) 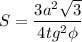
Объяснения:
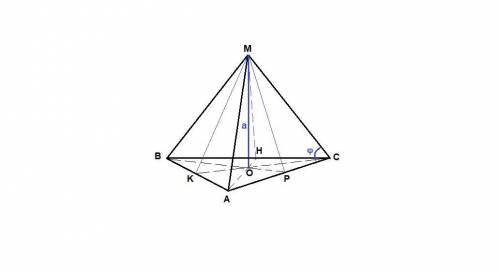
Пусть К, Н и Р - середины сторон АВ, ВС и АС соответственно, тогда
АН⊥ВС, ВР⊥АС, СК⊥АВ (треугольник правильный, медианы, высоты и биссектрисы совпадают).
Центр О правильного треугольника АВС равноудален от вершин и от сторон треугольника, т.е.
АО = ВО = СО, КО = НО = РО, а эти отрезки - проекции соответствующих наклонных на плоскость треугольника, значит
МА = МВ = МС - расстояния от точки М до вершин
и МК = МН = МР - расстояния от точки М до сторон (МК⊥АВ, МН⊥ВС, МР⊥АС по теореме о трех перпендикулярах).
а) ΔМОС: ∠МОС = 90°,
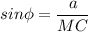
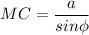
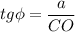
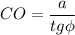
___
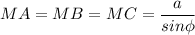
____
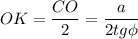 , так как медианы точкой пересечения делятся в отношении 2 : 1, считая от вершины.
, так как медианы точкой пересечения делятся в отношении 2 : 1, считая от вершины.
Из прямоугольного треугольника МОК по теореме Пифагора:
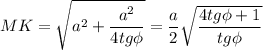
___
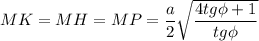
____
б) СО - радиус описанной окружности. Тогда длина окружности:
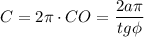
_____
в) 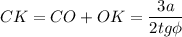
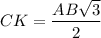
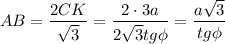
Площадь правильного треугольника АВС: