Точки f, o и t - соответственно середины ребер bc, dc и ac тетраэдра dabc. периметр треугольника fot равен 12 см. вычислите площадь боковой поверхности тетраэдра.
Тетраэдр это многоугольник состоящий из 4 граней, для решения задачи необходимо, чтобы все его рёбра были равны или какое-то ещё дополнительное условие, иначе для решения задачи не хватает данных.
F, O, T - середины ребер BC, DC, AC соответственно. Поэтому FO, OT, TF - средние линии треугольников CBD, CDA, CAB соответственно. А значит, BD=2FO, DA=2OT, AB=2TF.
ΔBDA - равносторонний (все рёбра тетраэдра равны), поэтому BD=DA=AB=24см:3=8см. Найдём площадь равностороннего треугольника по формуле , где a - сторона треугольника.
см².
Площадью боковой поверхности, будет площадь любых 3 граней (все грани это равные, равносторонние треугольники).
Прямокутник АВСД, діагоналі АС та ВД перетинаються в т. О. ОН - відстань від т. О до більшої сторони прямокутника ВС (отже ОН - висота трикутника ВСО) ОМ - відстань від т. О до більшої сторони прямокутника АД (отже ОМ - висота трикутника АДО) ОР - відстань від т. О до меншої сторони прямокутника АВ (отже ОР - висота трикутника АВО) ОК - відстань від т. О до меншої сторони прямокутника СД (отже ОК - висота трикутника СДО) Оскільки Діагоналі прямокутника мають однакову довжину, а також в точці перетину діляться навпіл, значить трикутник ВСО=трикутнику АДО та трикутник АВО=трикутнику СДО. А це означає, що і висоти у попарно рівних трикутниках між собою рівні, а саме ОК=ОР, а ОН=ОМ. Виходить, що ОН=ОМ=4 см та ОК=ОР=9 см (по умові задачі сказано, що точка перетину його діагоналей віддалена від його сторін на 4 см і на 9 см).
У прямокутника протилежні сторони рівні. АВ=СД=ОН+ОМ=4+4=8 см ВС=АД=ОР+ОК=9+9=18 см Периметр = сумі довжин усіх сторін прямокутника Периметр = АВ+ВС+СД+АД Отже Периметр = 8+18+8+18=52 см
Дано: АВ=СД=8см, ВС=6см, АД=16см, угол В = 45градусов. Решение: S=(a+b)делим на 2 и всё это умножаем на h-высоту. из точки В к основанию АД проводим высоту, обозначим её точкой К, высота будет перпендикулярна СД. Образуется треугольник АВК, в котором угол при к равен 90 градусов. значит, в треугольнике АВК: АВ=8см, АК=5см ( т.к. большее основание равно 16см, меньше равно 6, следовательно 16-6=10-сумма длин двух катетов при большем основании, 10:2=5-длина одного катета в треугольнике при большем основании). Чтобы найти площадь трапеции, нам надо знать длину высоты ВК(или h) (по-другому это будет неизвестный катет в прямоугольном треугольнике)., а чтобы узнать длину высоты,используем теорему Пифагора c^2=a^2+b^2. из этой теоремы находим неизвестный катет---> a^2=c^2-b^2. подставляем теперь числа к этой формуле: а^2=8^2 - 5^2 a^2=64-25 a^2=39 a=квадратный корень из 39-это высота h теперь найдём площадь трапеции: S=(6+16)/2 и умножаем на квадратный корень из 39 = 11 умноженное на корень из 39 ответ:S=11 умноженное на корень из 39
Тетраэдр это многоугольник состоящий из 4 граней, для решения задачи необходимо, чтобы все его рёбра были равны или какое-то ещё дополнительное условие, иначе для решения задачи не хватает данных.
F, O, T - середины ребер BC, DC, AC соответственно. Поэтому FO, OT, TF - средние линии треугольников CBD, CDA, CAB соответственно. А значит, BD=2FO, DA=2OT, AB=2TF.
ΔBDA - равносторонний (все рёбра тетраэдра равны), поэтому BD=DA=AB=24см:3=8см. Найдём площадь равностороннего треугольника по формуле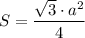 , где a - сторона треугольника.
, где a - сторона треугольника.
Площадью боковой поверхности, будет площадь любых 3 граней (все грани это равные, равносторонние треугольники).
S(бок.) =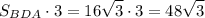 см².
см².
ответ: 48√3 см².