Признаки параллельности прямых.
1. Если при пересечении двух прямых секущей накрест лежащие углы равны, то прямые параллельны.
Доказательство:
Пусть О - середина отрезка АВ. Проведем ОН⊥b и продлим его до пересечения с прямой а.
ΔОАК = ΔОВН по стороне и двум прилежащим к ней углам (АО = ОВ, так как О - середина АВ, углы при вершине О равны как вертикальные, ∠ОАК = ∠ОВН по условию - накрест лежащие), значит
∠ОКА = ∠ОНВ = 90°.
Два перпендикуляра к одной прямой параллельны, значит
а║b.
2. Если при пересечении двух прямых секущей соответственные углы равны, то прямые параллельны.
3. Если при пересечении двух прямых секущей сумма односторонних углов 180°, то прямые параллельны.
Объяснение:
Косинус острого угла в прямоугольном треугольнике – это отношение прилежащего катета (b) к гипотенузе (с) (рис.1)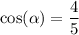
Значит Прилежащий катет b равен 4.
Гипотенуза c равна 5.
a) вычислите tg a
Тангенс острого угла в прямоугольном треугольнике – это отношение противолежащего катета к прилежащему.По теореме Пифагора найдём противолежащий катет а:
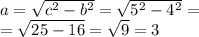
Тогда тангенс α:
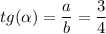
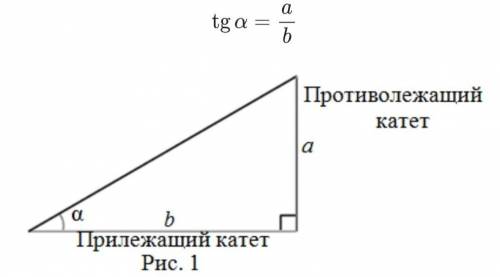
b) используя значение тангенса, постройте угол а
Строим прямоугольный треугольник с противолежащим углу А катетом 3
и прилежащим 4 (рис.2)

24:2=12