S полн = 72 см².
Объяснение:
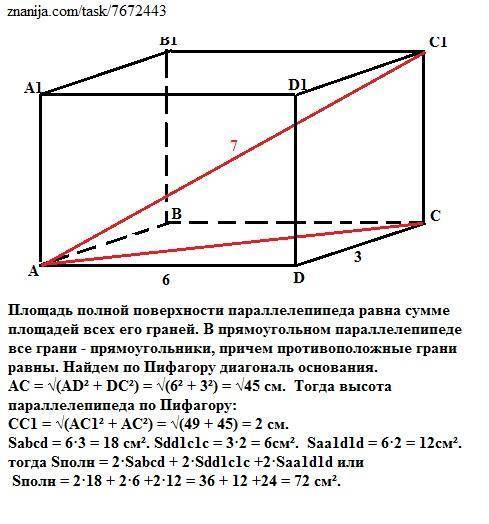
Площадь полной поверхности параллелепипеда равна сумме площадей всех его граней. В прямоугольном параллелепипеде все грани - прямоугольники, причем противоположные грани равны. Найдем по Пифагору диагональ основания.
АС = √(AD² + DC²) = √(6² + 3²) = √45 см. Тогда высота параллелепипеда по Пифагору:
СС1 = √(AС1² + АC²) = √(49 + 45) = 2 см.
Sabcd = 6·3 = 18 см². Sdd1c1c = 3·2 = 6см². Saa1d1d = 6·2 = 12см².
тогда Sполн = 2·Sabcd + 2·Sdd1с1с +2·Saa1d1d или
Sполн = 2·18 + 2·6 +2·12 = 36 + 12 +24 = 72 см².
Угол АСР - внешний и равен сумме двух внутренних, не смежных с ним. (смотри рисунок). Значит <CAB=20°. Тогда по теореме синусов в треугольнике АВС: ВС/sin20=AC/sin30, отсюда
АС=50*Sin30/Sin20 = 25/Sin20 (Sin30=1/2)
По таблице Sin20≈0,342. Sin50≈0,766.
В прямоугольном треугольнике РАС^
АР=АС*Sin50 или АР=25*0,766/0,342=55,99м.
АН=55,99+1,6=57,59 м Это ответ.