Диагональ (BD) параллелограмма делит его на два равных треугольника: \треугольник ABD = \треугольник CBD, так как сторона BD — общая , а \угол 1 = \угол 3 и \угол 4 = \угол 2 как накрест лежащие внутренние при параллельных прямых (AB || CD и AD || BC по определению параллелограмма) . В равных треугольниках AD = BC (так как \угол 1 = \угол 3), AB = CD (\угол 4 = \угол 2), \угол A = \угол C (лежат против BD). \угол ABC = \угол ADC (\угол 1 + \угол 2 = \угол 3 + \угол 4). Углы параллелограмма (например, \угол A и \угол ADC ), прилежащие к одной и той же стороне, являются внутренними односторонними при параллельных прямых (AB || DC, секущая AD) и в сумме составляют 180 градусов.
1) 
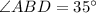; 2)
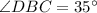
Объяснение:
Рассмотрим два решения (но при этом ответ не поменяется):
Обозначим данный угол буквами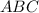 
.
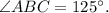
Проведём луч 
, перпендикулярный лучу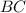 
.
.
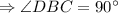угол, образованный данными лучами с другой стороной угла -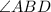 
.
Т.е.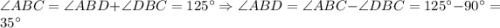 
Обозначим данный угол буквами .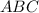
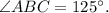
Проведём луч , перпендикулярный лучу 
.
.
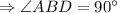угол, образованный данными лучами с другой стороной угла -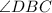 
.
Т.е.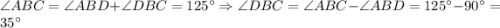 
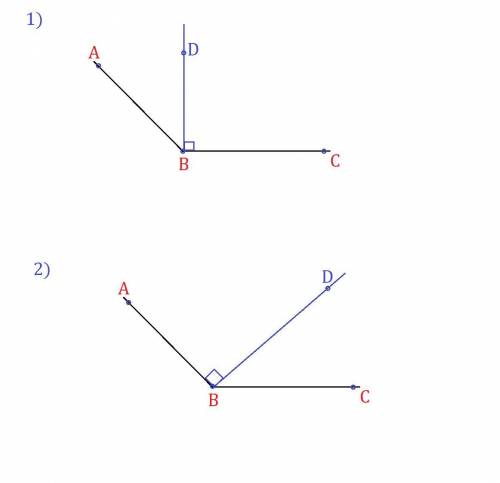
Треугольники АСМ и ВСМ - треугольники с одной высотой, проведенной из вершины С к стороне АВ. Следовательно, их площади относятся как основания, к которому проведена высота, то есть Sbcm/Sacm=1/2.
Сумма этих площадей - площадь треугольника АВС, которую найдем ао Герону: Sabc=√[p(p-a)(p-b)(p-c)], где р - полупериметр. p=(13+14+15):2=21.
Sabc=√(21*6*7*8)=84 см².
Тогда Sbcm=Sabc*(1/3) или Sbcm=84:3=28 см².