1. 15 см.
2. 31,75 см².
3. 36 м².
4. 21 кв. ед.
5. 113,4 см².
6. 6 см.
7. 50 см².
8. 27 см².
9. 7 см.
Объяснение:
1. Пусть меньший катет равен 2х. Тогда больший равен 5х.
S=1/2(ah)=1/2(2x*5x)=(1/2)10x²=5x²;
5x²=45;
x²=9;
х=±3; (-3 - не соответствует условию) .
х=3 см.
Больший катет равен 5х=5*3=15 см.
***
Площадь треугольника вычисляется по формуле:
S=1/2 ah;
S=12.7*5/2= 31.75см².
***
3. ABCD - прямоугольная трапеция. ∠А=∠В=90°. ВС=7 м, AD=11 м.
∠D=45°. Высота СЕ отсекает равносторонний треугольник СЕD, у которого ∠D=45°, CE⊥AD.
ED=CE=AD-BC=11-7=4 м.
S=h(a+b)/2=4(7+11)/2=2*18=36 м².
***
4. Есть несколько вычисления площадей фигур на клетчатой бумаге. Предложу свой.
Дополним параллелограмм до прямоугольника и вычтем площади дополнительных треугольников (см. приложение).
S=S(прямоугольника) - 2S(треугольника);
S=5*7-2(2*7)/2=35-14= 21 кв. ед.
***
5. S=ah, где а=16,2 см. Найдем h.
BE/AB=Sin 30°;
BE=AB*Sin30° =14*(1/2)=7 см.
S=16.2*7=113.4 см²
***
6. Площадь ромба по его диагоналям:
S=D*d/2;
d=2S/D=2*24/8=48/8=6 см.
***
7. Пусть сторона квадрата равна а см.
Найдем а: 5²= а²+а²; 2а²=5²; а=√(5²)/2=5√2 см;
S=a²=(5√2)²=50 см².
***
8. Пусть одна сторона равна х тогда вторая равна 3х.
Р(ABCD)=2(AB+BC);
2(x+3x)=24;
4x=12;
x=3 см - меньшая сторона (AB).
Большая сторона равна 3х=3*3=9 см (BC).
Площадь равна S=AB*BC=3*9=27 см².
***
9. S(ABC)=(1/2)AB*CE=1/2*14*10=70 см².
Ту же площадь можно найти по формуле:
S=1/2(BC*AF), где AF - высота, проведенная к стороне ВС
1/2(20*AF)=70;
20*AF=140;
AF=140/20=7 см.
Тупоугольный треугольник АВС
Угол А тупой
Сторона ВС = 4
Медианы АЕ, BF, CD
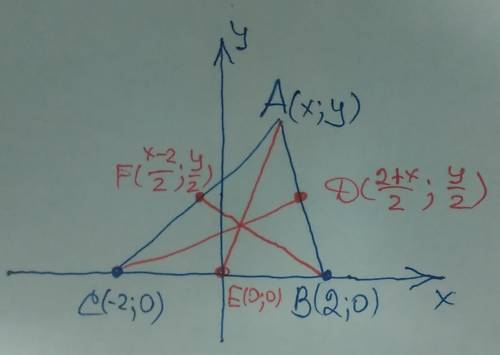
Координаты вершин
A(x;y)
B(2;0)
C(-2;0)
D((2+x)/2;y/2)
E(0;0)
F((x-2)/2;y/2)
Тупоугольным треугольник будет только если вершина А лежит внутри окружности, построенной на стороне CD и диаметром 4
AE² = x² + y² < 2²
|AE| < 2
Медиана АЕ меньше 2
Медиана ВF
ВF² = (2 – (x-2)/2)² + y²/4 = 1/4*(x² – 12x + y² + 36)
Медиана СD
CD² = ((2+x)/2+2)² + y²/4 = 1/4*(x² + 12x + y² + 36)
Сумма медиан CD и BF
S(x;y) = 1/2*sqrt(x² – 12x + y² + 36) + 1/2*sqrt(x² + 12x + y² + 36)
Производная по x, ищем экстремум
dS/dx = 1/4*((2(x - 6))/sqrt(x² - 12x + y² + 36) + (2(x + 6))/sqrt(x² + 12x + y² + 36)) = 0
(x - 6)/sqrt(x² - 12x + y² + 36) + (x + 6)/sqrt(x² + 12x + y² + 36) = 0
Числитель
(x - 6)*sqrt(x² + 12x + y² + 36) + (x + 6)*sqrt(x² - 12x + y² + 36) = 0
Тривиальное решение
х = 0 для любого y
Знаменатель при этом неважен, лишь бы оставался ненулевым
Это экстремум, но минимум или максимум — пока неизвестно.
Для определения проще всего вычислить значение S(0;2) и S(1;2)
S(0;2) = 1/2*sqrt(4 + 36) + 1/2*sqrt(4 + 36) = sqrt(40) ≈ 6,325
S(1;2) = 1/2*sqrt(1 – 12 + 4 + 36) + 1/2*sqrt(1 + 12 + 4 + 36) = 1/2*sqrt(29) + 1/2*sqrt(53) ≈ 6,333
Т.е. при x = 0 имеется минимум суммы длин медиан
Минимальной суммой медиан к боковым сторонам обладает равнобедренный треугольник
Производную по y можно не брать, т. к. по y сумма длин — функция возрастающая и максимальное значение суммы длин будет при максимальном значении y
Но из условия тупоугольности треугольника у нас y не может превосходить 2
Медиана к основанию тоже не превосходит 2, поэтому значение сумм длин всех трёх медиан будет не превосходить
S(0;2) + 2 = 2 + sqrt(40) ≈ 8,325
Что меньше требуемых по условию 9
тогда <ВОС=3х°
имеем х°+3х°=120°
4х=120 х=30°
значит <АОС=30°
<ВОС=3×30=90°