Объяснение:
а) по теореме Пифагора найдём гипотенузу АВ: АВ²=АС²+ВС²
АВ=√(8²+6²)=√(64+36)=√100=10см
Зная, что центр описанной окружности около прямоугольного треугольника, является середина его гипотенузы. Поэтому R=AB÷2
R=10÷2=5см;
ответ: R=5см
б) катет, лежащий напротив угла 30° равен половине гипотенузы, поэтому гипотенуза АВ будет в 2 раза больше него: АВ=АС×2; АВ=18×2=36см;
Также R=AB÷2; R=36÷2=18.
ответ: R=18см
От себя добавлю что если вычислять по формуле, которая дана в задании, то результат получается другой. Например: следуя ей и используя данные задания "а", получится следующее: R=(a+b-c)÷2=(8+6-10)÷2=
=(14-10)÷2=4÷2=2. Совсем другой результат. Правило, что центр описанной окружности в прямоугольном треугольнике является середина гипотенузы, верно
ФОРМУЛА НА САМОМ ДЕЛЕ ТАКАЯ:
R=½×√(a²+b²), где " а" и "b"- катеты
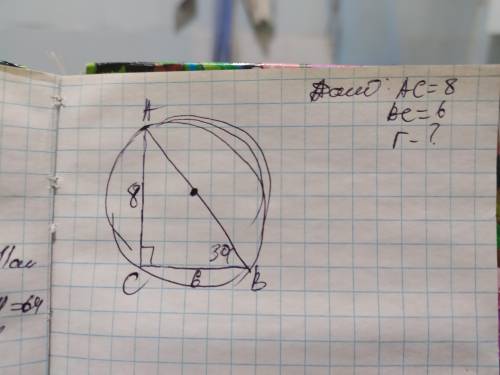
∠KMC=180-∠ HKM-∠MHK=180-23-90=67°
∠MKC=∠ HKM+∠HKC=23°+44°=67°
∠MCK=180°-∠KMC-∠MKC=180-67-67=46°
Т.к. два угла раны (∠KMC=∠MKC), значит треугольник равнобедренный
По основанию см. комментарий к заданию
2) Высота СD делит ∠MCK пополам, т.е. ∠MCD=∠DCK=46/2=23°
∠HOC=∠COB=180°-∠MCD-∠CHO=180°-90°-23°=67°
∠BOK=180°-∠OKB-∠OBK=180°-90°-44°=46°
∠KOC=∠COB+∠BOK=67°+46°=113°
Рисунок прилагается