Объяснение:
1. Средняя линия треугольника парраллельна стороне и равна его половине,
Тогда если средние линии треугольника относятся как 2:2:4, то стороны относятся как 4:4:8
4х+4х+8х=45
16х=45
х = 45/16
4х = 45/16*4 = 45/4 = 11,25
8х = 11,25*2 = 22,5
ответ: 11,25 см, 11,25 см, 22,5 см
2. Назовём медиану, проведённую из точки B, BD.
Медианы в треугольнике делят друг друга в отношении 2 : 1, считая от вершины, то есть BO : OD = 2 : 1
Так как прямые EF и AC параллельны, то ∠BAC = ∠BEF как соответственные углы.
Рассмотрим ΔABC и ΔEBF
1) ∠B - общий
2) ∠BAC = ∠BEF - из решения
Отсюда следует, что эти треугольники подобны.
Коэффициент подобия будет равен отношению BD и BO
k = BD : BO = 3x : 2x = 3 : 2
Из подобия AC : EF = 3 : 2
15 : EF = 3 : 2
3EF = 30
EF = 10 см
ответ: 10 см
3. Учитывая, что согласно теореме Пифагора сумма квадратов катетов равна квадрату гипотенузы, вычисляем длину гипотенузы АВ прямоугольного треугольника АВС:
АВ^2 = АС^2 + ВС^2
АВ - √АС^2 + ВСАС^2 = √5^2 + (5√3)^2 = √25 + 25 х 3 = √100 = 10 сантиметров.
Отношение катета АС к гипотенузе АВ является синусом угла АВС.
Синус угла АВС = АС/АВ = 5 : 10 = 1/2.
Угол АВС = 30°.
ответ: длина гипотенузы АВ равна 10 сантиметров, угол АВС = 30°.
4. Так как ВН высота треугольника АВС, то треугольники АВН и ВСН прямоугольные.
В прямоугольном треугольнике ВСН определим величину катета ВН через гипотенузу и противолежащий ВН угол.
Sinβ = ВН / ВС.
ВН = ВС * Sinβ = 7 * Sinβ см.
В прямоугольном треугольнике АВН выразим величину катета АН через катет ВН и угол ВАН.
tgα = BH /AH.
AH = BH / tgα = 7 * Sinβ / tgα см.
ответ: Длина отрезка АН равна 7 * Sinβ / tgα см.
5. Рассмотрим треугольник АКД, у которого, по условию, точка В середина отрезка АК, то есть АВ = ВК и так как ВС параллельна АД, как основания трапеции, тогда отрезок ВС является средней линией треугольника.
Длина средней линии треугольника равна половине длины параллельной ей стороны.
ВС = АД / 2 = 12/2 = 6 см.
Так как средняя линия треугольника совпадает с малым основанием трапеции, то сумма сторон трапеции будет равна 12 + 6 = 18 см.
ответ: Сумма оснований трапеции равна 18 см.
Линия пересечения плоскости AD₁C₁ и плоскости основания есть ребро параллелепипеда АВ.
Угол между плоскостью AD₁C₁ и плоскостью основания есть угол между плоскостью AD₁C₁ перпендикуляром к АВ, то есть высотой ромба. На рисунке обозначена как ВН.
ΔСВН - прямоугольный, с прямым углом Н, по условию острый угол ромба-основания равен 60⁰, отсюда, зная sin60⁰ находим высоту ромба ВН:
а) 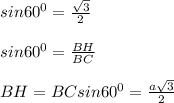
Можно было вычислить и так, как мы находили АН во вчерашнем задании, через т. Пифагора, зная, что СН=а/2, как катет, лежащий против угла в 30⁰, но сегодня решаем так, чтобы показать разные пути решения.
б) Высоту параллелепипеда HH₁находим из прямоугольного ΔВН₁Н в котором угол Н прямой, угол В=60⁰, и зная значение tg60⁰:
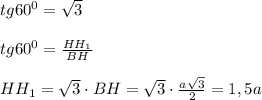
в) Найти площадь боковой поверхности - самая простая часть этого задания:
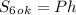 , где
, где 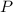 и
и  - периметр основания и высота пераллелепипеда соответственно.
- периметр основания и высота пераллелепипеда соответственно.

г) 
Угол abm 30 градусов
Am 6 сантиметров
Найти:
Bd
Решение:
Т.к. треугольник abm прямоугольный то ab будет 12см ( на против угла в 30 гр. Лежит угол равный половине гипотенузы) т.к.abcd ромб ab=ad =12см.
12-6=6см
Угол b= 180-30=120
120÷2=60 (bd биссектриса)
60-30=30=> bd =12си