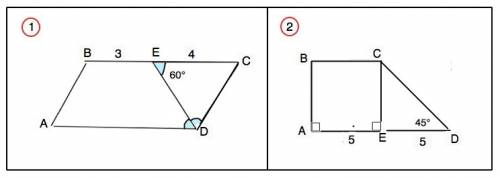
1) В параллелограмме противолежащие стороны равны и параллельны, противолежащие углы равны.
ДЕ - биссектриса, ⇒∠ЕDА=∠ЕDС.
∠СЕD=∠ЕDА – накрестлежащие. ⇒
треугольник СЕD равнобедренный, а так как углы при основании ЕD равны 60°, он - равносторонний.
Угол С=60°, угол А=угол С=60°. Сумма углов параллелограмма, прилежащих к одной стороне, равна 180°. ⇒∠В=∠D=120°
СD=ЕС=АС=4 см. АD=ВС=3+4=7 см
Р (АВСD)=2•(7+4)=22 см
Четырехугольник АВЕD - равнобедренная трапеция, так как ВЕ║|АD, и АВ=СД⇒АВ=ЕД.
-------------------
2) ∆ СЕD прямоугольный, Сумма острых углов прямоугольного треугольника 90°. ⇒
угол ЕСD=90°- 45*=45°⇒ ∆ СЕD – равнобедренный.
CE=ED=5
Перпендикуляр СЕ параллелен и равен АВ. -⇒
АВ=СЕ=5 см
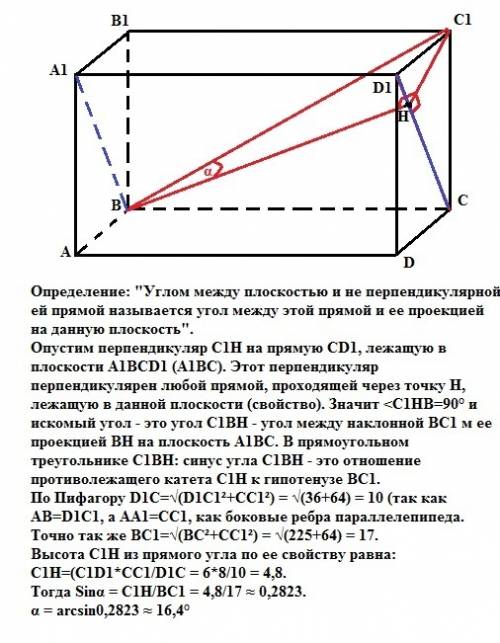
Определение: "Углом между плоскостью и не перпендикулярной ей прямой называется угол между этой прямой и ее проекцией на данную плоскость".
Опустим перпендикуляр С1Н на прямую СD1, лежащую в плоскости А1ВС (это плоскость А1ВСD1, так как секущая плоскость пересекает параллельные плоскости АА1В1В и DD1C1C по параллельным прямым А1В и D1C). Отрезок С1Н перпендикулярен любой прямой, проходящей через точку Н, лежащую в данной плоскости (свойство). Значит <C1HB=90° и искомый угол - это угол С1ВН - угол между наклонной ВС1 м ее проекцией ВН на плоскость А1ВС. В прямоугольном треугольнике С1ВН: синус угла С1ВН - это отношение противолежащего катета С1Н к гипотенузе ВС1.
По Пифагору D1C=√(D1C1²+CC1²) = √(36+64) = 10 ед (так как АВ=D1C1, a AA1=CC1, как боковые ребра параллелепипеда.
Точно так же ВС1=√(ВC²+CC1²) = √(225+64) = 17 ед.
Высота С1Н из прямого угла по ее свойству равна:
С1Н=(С1D1*CC1/D1C = 6*8/10 = 4,8 ед.
Тогда Sinα = C1H/BC1 = 4,8/17 ≈ 0,2823.
α = arcsin0,2823 ≈ 16,4°.
(-3)+4=1, а (-2)+(-1)=-3