1) 30*. 30*. 120*.
2) 40*. 80*. 60*.
3) 12 см. 24 см. 24 см.
Объяснение:
1. ∠2+∠4 = 180*
∠4=5∠2;
∠2 + 5∠2 =180*;
6∠2 = 180*;
∠2 = 180* : 6 = 30*.
∠4 = 5*30=150*.
∠1=∠2 = 30* - углы при основании равнобедренного треугольника.
∠3=180-2*30* = 180*-60*=120*.
***
2. Дано. ∠1:∠2:∠3=2:4:3;
Найти ∠1, ∠2, ∠3.
Решение.
Сумма углов треугольнике равна 180*
Пусть ∠1 = 2х.
Тогда ∠2=4х, ∠3=3х.
2х+4х+3х=180*;
9x=180*;
x=180* :9 = 20*.
Тогда
∠1=2х = 2*20 = 40*.
∠2 = 4х = 4*20=80*.
∠3= 3х = 3*20=60*.
***
3. Дано. АВС - равнобедренный треугольник. Р=60см. Одна сторона равна 12 см. Найти все стороны.
Решение.
Пусть стороны равны a, b, c.
Периметр Р=a+b+с, где a=b. c=12 см. Тогда:
2a + 12 =60;
2а=60-12;
2а=48;
а=b= 24 см.
А4. 4 120°
А5. 1 10
A6. 1 16
A7. 2 6√5
А4. Угол тупой: значит 150° или 120°
S=1/2 AB*AC sin α;
3√3=1/2 *6*2sin α;
sinα=√3/2; α=120°
A5.
Если известно две стороны треугольника и угол между ними, то площадь данного треугольника вычисляется, как половина произведения этих сторон умноженная на синус угла между ними.
угол тупой sin 150=1/2
значит α=120
или 3√3=6*2sinα/2→sinα=√3/2, α=120°
А5.
Высота, проведенная к основанию, делит его на две равные части, и косинус искомого угла становится равен половине основания, деленного на боковую сторону: cosα=b/(2a), где а- боковые стороны
√0,91=2√91/2а; а=√91/√0,91=10
A6. S=pr, де р=Р/2
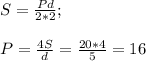
A7. Когда известны стороны ищем площадь по формуле Герона
Найдём полупериметр
р=(4+7+9)/2=10
Если ты сама не напишешь дано , найти и ответ к каждой задаче- то больше не буду! Да, и формулу Герона найди и выпиши перед решением
Количество ребер, выходящих из каждой вершины многогранника, не меньше трех.
Примем количество вершин равным а. Тогда ребер из всех вершин будет 3а. Но количество ребер посчитано дважды, т.к. одно ребро соединяет две вершины. Значит, всего ребер должно быть вдвое меньше. И тогда количество ребер 3а/2=х
3а=2•х. Но число 2017 – простое, не имеет других делителей, кроме единицы и самого себя. Поэтому 2017≠2х, независимо от того, сколько ребер выходят из каждой вершины многогранника.
Следовательно, многогранник с таким количеством ребер не существует.