Точка пересечения биссектрис АМ и ДМ, очевидно, находится на стороне ВС.
Угол АМВ = угол МАД (накрест лежащие углы для параллельных ВС и АД, секущей АМ) , угол АМВ = угол МАД (так как АМ - биссектриса) .
Треугольник АВМ равнобедренный, АВ = ВМ.
Угол СМД = угол АДМ (накрест лежащие углы для параллельных ВС и АД, секущей ДМ) , угол АДМ = угол СДМ (так как ДМ - биссектриса) .
Треугольник СМД равнобедренный, СМ = СД.
АВ = СД (противоположные стороны параллелограмма) .
Поэтому АВ = ВМ = СМ, ВС = ВМ + СМ = 2*АВ.
Периметр 2*(АВ + ВС) = 2*3*АВ = 36 см.
АВ = 6 см, ВС = 12 см.
Длины всех ребер правильной шестиугольной призмы равны. Вычислителе длину большей диагонали призмы, если известно, что площадь боковой поверхности призмы равна 96 см².
Площадь боковой поверхности правильной шестиугольной призмы находится по формуле:
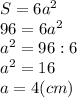
а - ребро нашей призмы.
Обратим внимание на чертеж. Искомая длина большей диагонали есть длина гипотенузы прямоугольного треугольника АА₁D.
AD = 2 * 4 = 8 (см)
По теореме Пифагора:
с² = a² + b²
AD₁² = AD² + DD₁²
AD₁² = 8² + 4²
AD₁² = 64 + 16
AD₁² = 80
AD₁ = √(16*5) = 4√5 (см)
ответ: 4√5 см

АК = АЕ = 6*cos 30° = 6*(√3/2) = 3√3 см.
Отрезок КЕ как средняя линия треугольника равен 6/2 = 3 см.
Площадь полученного сечения можно определить пр формуле Герона:
S = √(p(p-a)(p-b)(p-c)).
Периметр равен 2*3√3 + 3 = 6√3 + 3 = 3(2√3 + 1) см.
Полупериметр р = Р/2 = 1,5(2√3+ 1) ≈ 6,696152 см.
Подставив полученные результаты в эту формулу, получаем:
S = 7,462405778 см².