в координатах скалярное произведение
a1*a2=3*4+4*3=24
|a1|^2=3^2+4^2=25
|a1|=5
|a2|^2=4^2+3^2=25
|a2|=5
скалярное произведение через длины векторов и угол между ними
a1*a2=|a1|*|a2|*cosx=5*5*cosx
так как это одно и тоже скалярное произведение. приравняю их
24=25*сosx
cosx=24/25=0.96
S = 4(7√3+6) см²
Р = 22+4√3(1+√2) см.
Объяснение:
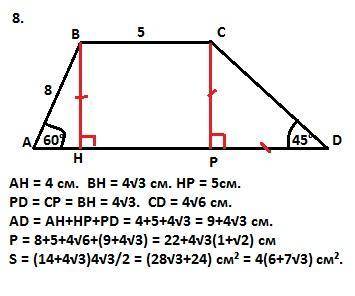
АВCD - трапеция. Опустим высоты ВН и СР на основание AD. В прямоугольном треугольнике АВН катет АН лежит против угла 30° (по сумме острых углов прямоугольного треугольника) и равен половине гипотенузы АВ. Второй катет ВН найдем по Пифагору: ВН=√(АВ²-АН²). Тогда
АН = 4 см. ВН = √(8²-4²) = 4√3 см.
CР = ВН (высота трапеции) => PD = CР (как катеты равнобедренного прямоугольного треугольника (острые углы равны по 45° - дано).
CD = √(2·BH²) = 4√6 см. (по Пифагору).
AD = AH+HP+PD = 4+5+4√3 = (9+4√3) см.
Тогда S = (BC+AD)·BH/2 = (14+4√3)·4√3/2 = (28√3 + 24)см²
Периметр Р = 8+5+4√6+(9+4√3) = 22+4√3(1+√2) см.
Дано:
Прямоугольный треугольник
Меньший катет-3
Больший катет -4
Найти V-?
S полной поверхности-?
Решение
Тело вращения - прямой конус, где больший катет - высота (Н) конуса, меньший катет - радиус (R) основания конуса, гипотенуза треугольника - образующая (L) конуса.
Сначала нацдем по теореме Пифагора образующую
R² + H² = L²
3² + 4² = L²
L² = 9 + 16
L³ = 25
L = 5 (см)
Площадь боковой поверхности конуса равна произведению числа π на радиус окружности основания и на длину образующей конуса
S = π * R * L
S = π * 3 * 5 = 15π
Объем конуса равен одной трети произведения числа π на квадрат радиуса основания на высоту.
V = 1/3 * π * R² * H
V = 1/3 * π * 3² * 4 = 1/3 * 9 * 4 * π = 12π
ответ: S=15п, V=12п
α = 74°
Объяснение:
1)
Пусть a = {3; 4}; b = {4; 3}
Скалярное произведение
(a, b) = 3*4 + 4*3 = 24
2)
Длины векторов:
| a | = √ ( 3² + 4²) = √ (9+16) = √ 25 = 5
| b | = √ ( 4² + 5²) = √ (16 + 9) = √ 25 = 5
3)
cos α = (a, b) / ( |a| * |b|) = 24 / (5*5) = 24/55 = 0,96
α ≈ 74°