ответ: 80.
Объяснение:
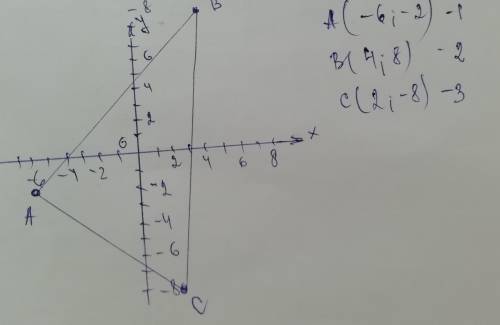
Построим координатную плоскость и нанесем точки А,В,С. (смотри чертёж).
Чтобы найти площадь при таких данных, воспользуемся формулой Герона:
S = √p(p-a)(p-b)(p-c), где a, b и c - стороны треугольника р=(a+b+c)/2 - полупериметр треугольника.
Но есть более простая формула:
S=1/2|(x2-x1)(y3-y1)-(x3-x1)(y2-y1|); (| | - по модулю);
Обозначим точки 1 - А; 2 - В; 3 - С.
Тогда S= 1/2| (4-(-6))(-8-2)-(2-(-6))(8-(-2))|=1/2| (10*(-6))-(10*10)|=1/2| (-60-100) |= 1/2 |-160|=1/2* 160=80.
∪AB+∪ACB=360°
Вписанный угол С равен половине дуги, на которую опирается.
∪AB= 2∠С =240°
O - центр описанной окружности. Центральный угол AOB равен дуге, на которую опирается.
∠AOB= ∪ACB =360°-∪AB =120°
AO, OB - радиусы описанной окружности. По теореме косинусов
AB^2= 2r^2 -2r^2·cos120° <=> AB^2= 3r^2 <=> r=AB/√3 =22