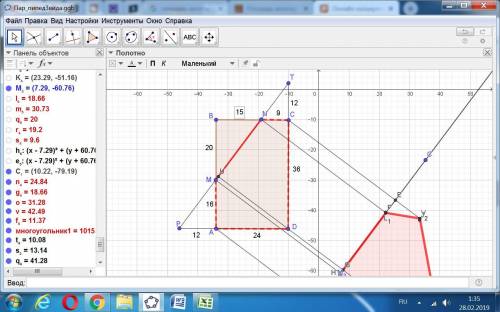
В соответствии с заданием определяем отрезки:
BM:MA=5:4 = (36/9)*5 = 20:16.
BN:NC=5:3 = (24/8)*5 = 15:9.
То есть, от основания отсекается треугольник площадью (1/2)*20*15 = 150 кв.ед.
Оставшаяся площадь равна (24*36) - 150 = 864 - 150 = 714 кв.ед.
Эта площадь равна проекции заданного сечения на основание.
Теперь найдём угол наклона секущей плоскости.
Прямая, проходящая через точки M и N, образует подобные треугольники с продолжениями сторон АД и СД.
По Пифагору определяем длину MN = 25. Синус угла NТС =3/5, а косинус 4/5, тангенс 3/4. Отрезок ТС = 9/(3/4) = 12.
ДТ = 36 + 12 = 48. Проекция высоты из точки Д1 на MN равна 48*(3/5) = 144/5 = 28,8. Так как высота ДД1 тоже равна 28,8, то угол наклона секущей плоскости равен 45 градусов.
Площадь сечения равна:
S = 714/cos 45° = 714/(√2/2) = 714*√2 ≈ 1009,75 кв.ед.
Доказательство деления ребра АА1 этой плоскостью:
вытекает из подобия треугольников РКА и РД1Д: КА/12 = 28,8/(12+24), отсюда КА = 12*28,8/36 = 28,8/3. То есть АА1 делится на 3 части, а АК составляет 1 из 3 частей, то есть отношение равно 1:2.
Аналогично для ребра ДД1 отношение 1:3.
Объяснение:
Начертить прямую произвольной длины.
С циркуля и линейки возвести перпендикуляр, равный данной высоте.
( Это одно из простейших построений, Вы наверняка умеете его делать)
Обозначить основание перпендикуляра Н, а свободный конец - В. Это вершина треугольника.
Раствором циркуля, равным длине одной из сторон, из В, как из центра, провести полуокружность до пересечения с первой прямой.
Точку пересечения обозначить А.
Соединив А и В, получим сторонуАВ.
Точно так же отложить вторую сторону раствором циркуля, равным ее длине.
Обозначить точку пересечения дуги с прямой С и соединить с В.
Можно несколько иначе построить вторую сторону.
От А отложить длину второй известной стороны.
Свободный конец обозначить С.
Соединив С и В, получим сторону ВС.
Треугольник по двум сторонам и высоте построен.
По теореме Пифагора найдём высоту
CH = √(BC²-BH²) = √(26²-24²) = √((26-24)*(26+24)) = √(2*50)= √100 = 10
cos A = CH/BC = 10/26 = 5/13
13 cos A = 5