Коэффициент подобия называется отношение любых соответственных линейных размеров первой фигуры к линейным размерам второй фигуры, находящимся против одинаковых углов.
А так как площадь треугольника равна произведение сторон АВ, ВС, и синуса угла между ними, а А1В1 = к * АВ, В1С1 = к * ВС, к коэффициент подобия,то :
S A1B1C1 = A1B1 * B1C1 * sin <(A1B1,B1C1) = 81 (cм2) = к* АВ * к * ВС * sin<(AB,BC) = k^2*S ABC
S ABC = AB * BC * sin < (AB,BC)=25(cм2).
к^2 = S A1B1C1/ S ABC = 81/25, k = 9/5 = 1,8
^ - степень
/ - деление
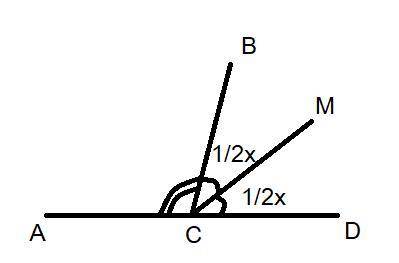
Допустим, что угол АСМ - это 3х, а угол ВСD ⇒ х.
В сумме углы АСМ и ВСD минус угол МСD дают 180°.
Логично, что если угол BCD - это х, то его половинки - это х/2.
Составим уравнение.
3х+х-х/2=180°
При выполнении несложных математических расчётов получается, что х(угол BCD)=51 3/7°
Следовательно, угол АСВ=180°-51 3/7°=128 4/7°
ответ: 51 3/7° и 128 4/7°.
(это то, что записано в условии. ответы странные, странные и смежные углы... АВС и ВСD не могут быть смежными. смежными могут быть только АСВ и ВСD, как указано в вопросе к задаче... смотри ещё раз условие внимательнее)
Угол С – угол между векторами АС и ВС.
1) Найдем координаты векторов АС и ВС.
Чтобы найти координаты вектора, нужно найти разность соответствующих координат точки конца вектора и начала.
Найдем координаты вектора АС:
АС (хс – ха; ус – уа);
АС (4 – 1; 5 – 1);
АС (3; 4).
Найдем координаты вектора ВС:
ВС (хС – хВ; уС – уВ);
ВС (4 – 4; 5 – 1);
ВС (0; 4).
2) Скалярное произведение векторов:
АС * ВС = 3 * 0 + 4 * 4 = 0 + 16 = 16.
3) Найдем длины векторов АС и ВС.
Квадрат длины вектора равен сумме квадратов его координат.
Найдем длину вектора АС:
|АС|2 = 32 + 42 = 9 + 16 = 25;
|АС| = 5.
Найдем длину вектора ВС:
|ВС|2 = 02 + 42 = 16;
|ВС| = 4.
4) Найдем косинус угла между векторами:
cos С = АС * ВС / (|АС| *|ВС|) = 16 / (5 * 4) = 4/5 = 0,8.
ответ: 0.8