
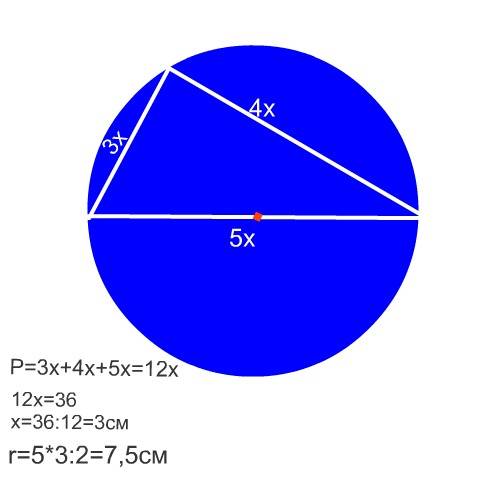
Гипотенуза этого прямоугольного треугольника является диаметром окружности.
Так как отношение катетов 3:4, то гипотенуза в этом отношении будет 5,
т.е все стороны треугольника относятся как 3:4:5, поскольку этот треугольник - египетский.
Примем коэффициент отношения сторон за х
тогда его периметр равен
3х+4х+5х=12х
Коэффициент равен 36:12=3
Диаметр круга
3*5=15 см
Радиус 15:2=7,5 см
-------------------------------
Боковую сторону можно найти через синус угла при вершине треугольника.
Он равен 180-2а
х=h: sin(180-2а)
Если плоскость сечения проведена через А1В1, то линия ЕК сечения основания АВС параллельна А1В1.
Пусть точка О - центр основания АВС.
Высота СР проходит через точку О и делится ею в отношении СО/ОР = 2/3. Также из условия подобия ЕК = (2/3)АВ = (2/3)*6 = 4.
Отрезок ОР = (1/3)СР = (1/3)*6*(√3/2) = √3.
В сечении имеем равнобокую трапецию ЕА1В1К.
Находим её высоту OМ = √(ОР² + РМ²) = √(3 + 13) = √16 = 4.
Получаем ответ: S = EK*OM = 4*4 = 16 кв.ед.