ЛУЧШИЙ ОТВЕТ☆
Объяснение:
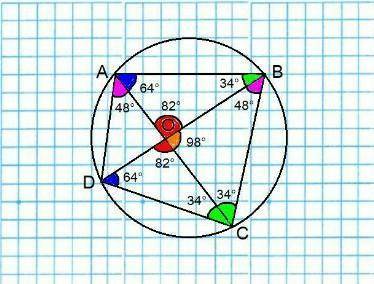
ответ: ∠A = 112° ; ∠B = 82° ; ∠C = 68° ; ∠D = 98°.
Объяснение: Обозначим середину окружности буквой O.
∠CBD и ∠CAD - вписанные (углы, у которых вершина на окружности, а стороны пересекают окружность).
Вписанные углы, опирающиеся на одну и ту же дугу, равны.
⇒ ∠CBD = ∠CAD = 48°.
COD - треугольник.
Сумма внутренних углов треугольника равна 180°.
⇒ ∠DOC = 180° - (64° + 34°) = 180° - 98° = 82°.
Сумма смежных углов равна 180°.
⇒ ∠BOC = 180° - 82° = 98°.
COB - треугольник.
Сумма внутренних углов треугольника равна 180°.
⇒ ∠OCB = 180° - (98° + 48°) = 180° - 146° = 34°.
⇒ ∠C = 34° * 2 = 68°.
Если четырёхугольник можно вписать в окружность, то сумма противоположных углов этого четырёхугольника равна 180°.
⇒ ∠A = 180° - 68° = 112°.
Если ∠CAD = 48° и ∠A = 112° ⇒ ∠CAB = 112° - 48° = 64°.
Вертикальные углы равны.
⇒ ∠DOC = ∠AOB = 82°.
AOB - треугольник.
Сумма внутренних углов треугольника равна 180°.
⇒ ∠ABO = 180° - (64° + 82°) = 180° - 146° = 34°.
⇒ ∠B = 34° + 48° = 82°.
Если четырёхугольник можно вписать в окружность, то сумма противоположных углов этого четырёхугольника равна 180°.
⇒ ∠D = 180° - 82° = 98°.
В чём вопрос?
Объяснение:
В чём вопрос?В чём вопрос?В чём вопрос?В чём вопрос?В чём вопрос?В чём вопрос?В чём вопрос?В чём вопрос?В чём вопрос?В чём вопрос?В чём вопрос?В чём вопрос?В чём вопрос?В чём вопрос?В чём вопрос?В чём вопрос?В чём вопрос?В чём вопрос?В чём вопрос?В чём вопрос?В чём вопрос?В чём вопрос?В чём вопрос?В чём вопрос?В чём вопрос?В чём вопрос?В чём вопрос?В чём вопрос?В чём вопрос?В чём вопрос?В чём вопрос?В чём вопрос?В чём вопрос?В чём вопрос?В чём вопрос?В чём вопрос?В чём вопрос?В чём вопрос?В чём вопрос?В чём вопрос?В чём вопрос?В чём вопрос?В чём вопрос?В чём вопрос?В чём вопрос?В чём вопрос?В чём вопрос?В чём вопрос?В чём вопрос?В чём вопрос?В чём вопрос?В чём вопрос?В чём вопрос?В чём вопрос?В чём вопрос?В чём вопрос?В чём вопрос?В чём вопрос?
AC/AB=6/5
AC=6x, AB=BC=5x
Pabc=5x+5x+6x
32=5x+5x+6x
32=16x
x=32/16
x=2
AC=6*2=12 см
AB=BC=5*2=10 см
Проведем высоту ВМ перпендикулярно АС. ВМ - высота, медиана, биссектриса (т.к. ∆АВС равнобедренный)
АМ=МС=АС/2=12/2=6 см
В ∆АВМ ВМ=√(АВ²-АМ²)=√(10²-6²)=√(100-36)=√64=8 см
Sabc=(BM*AC)/2=(8*12)/2=96/2=48 см²
ответ: 48 см²