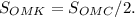
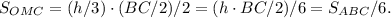
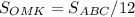. Т.к. стороны треугольника OMK равны трети длин медиан, то площадь треугольника, составленного из медиан в 9 раз больше площади треугольника OMK, т.е. она равна 
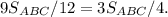Поэтому искомое отношение площади треугольника ABC, к площади треугольника, составленного из его медиан равно 4/3.
Ив
оч Ек
Ость
Это суффиксы