8. <DBC=63°
9. P = 36 ед.
10. Не полное условие.
Объяснение:
Дуга BD равна 2*27° = 54° (так как вписанный угол, опирающийся на эту дугу, равен половине градусной меры этой дуги).
Дуга BDAC = 180°, так как ВС - диаметр.
Дуга DAC = DDAC - BD = 180-54 = 126°. =>
<DBC = 63° (вписанный, равен половине градусной меры дуги, на которую он опирается).
9. Биссектрисы углов параллелограмма отсекают от него равнобедренные треугольники. В нашем случае эти биссектрисы имеют общую точку Е на стороне ВС. Значит
АВ = ВЕ и EC = CD => BC = 2AB.
AB = СD и BC = AD (противоположные стороны параллелограмма).
Рabcd = 6*AB = 36 ед.
ответ:ответ, проверенный экспертом
4.0/5
13
KuOV
главный мозг
4.9 тыс. ответов
26.7 млн пользователей, получивших
Объяснение:
a)(Фото)
https://ru-static.z-dn.net/files/dd9/6dbd3d984a1b49a60897ad7ac129c92c.png
b)Тангенс острого угла прямоугольного треугольника - это отношение противолежащего катета к прилежащему.
Значит надо построить прямоугольный треугольник, отношение катетов которого равно 1:4. Угол, лежащий против меньшего катета будет искомым.
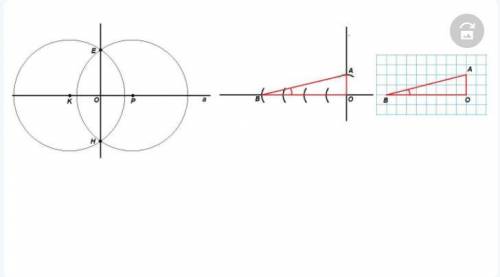
Если это не задача на построение, то можно построить треугольник по клеточкам тетради так, чтобы один катет был равен, например, одному сантиметру, а другой - 4 см. Тогда угол, лежащий против катета в 1 см - искомый. На рисунке это ∠АВО.
Если задача на построение, то
строим две перпендикулярные прямые, для этого
проводим прямую а, отмечаем на ней две произвольные точки К и Р; проводим две окружности с центрами в этих точках произвольного одинакового радиуса, большего половины отрезка КР; через точки пересечения этих окружностей Е и Н проводим прямую. ЕН⊥а. О - точка пересечения прямых.
от точки О с циркуля откладываем равные отрезки вверх один (точка А), влево - 4 (точка В).
соединяем получившиеся точки;
∠АВО - искомый.
https://ru-static.z-dn.net/files/dbc/dd6b3aac185aecfed037c2300250715f.png

S=(10+6)/2*5=40