Определение: Параллелепипед — многогранник, у которого шесть граней и каждая из них — параллелограмм.
Требуется доказать, что противоположные грани параллелепипеда параллельны и равны.
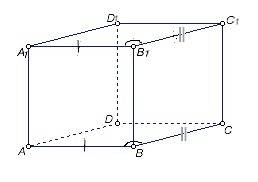
Докажем на примере оснований АВСD и A1B1C1D1 данного параллелепипеда.
Отрезки А1В1 и АВ параллельны и равны как стороны параллелограмма АА1В1В, отрезки В1С1 и ВС параллельны и равны как стороны параллелограмма ВСС1В1. ⇒
плоскости оснований параллельны по двум пересекающимся прямым.А1В1 и В1С1 одной плоскости и АВ и ВС противоположной.
Стороны параллелограммов АВСD и A1B1C1D1 равны , соответственные стороны углов А1B1C1 и ABC образованы параллельными прямыми,⇒ углы равны – эти параллелограммы равны, (их можно совместить наложением). Аналогично доказывается параллельность и равенство остальных граней. Доказано.
S₁ = a² = 36
a = √36 = 6 см
Площадь боковой поверхности - это площадь 4-х равнобедренных треугольников с основанием a и высотой, равной апофеме f
S₂ = 4*1/2*a*f = 60
a*f = 30
f = 30/a = 30/6 = 5 см