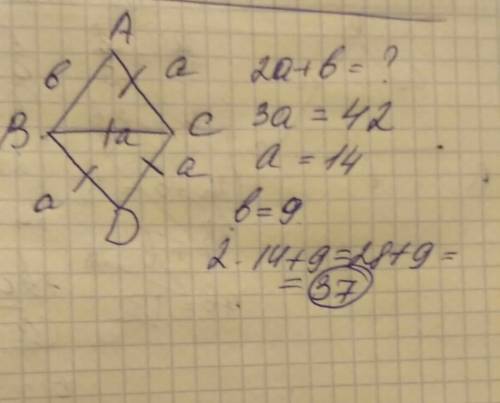
Объяснение:
У ромба 2 пары равных внутренних углов, сумма которых равна 360°.
Пусть тупой угол равен 2х, тогда острый будет х. Получаем: 2*2х+2х=360
6х=360
х=60.
Значит острый угол ромба равен 60°, а тупой 120°.
Площадь ромба равна половине произведения его диагоналей.
Найдем диагонали.
Известно, что диагонали ромба делят внутренние углы пополами и пересекаются под прямым углом. Исходя из этого, приняв, что диагонали ромба пересекаются в точке О и ∠АВС - тупой, рассмотрим ΔВСО.
Он прямоугольный с ∠ОСВ= 30° и ∠ОВС=60° при гипотенузе ВС. Значит его катет ВО = ВС·sin30° = 3√3,
катет СО=ВС·sin60° = 6√3 · √3 ÷2 = 9
Мы определили длины половин диагоналей ромба.
Тогда площадь ромба АВСD равна
3√3 × 9 × 2 = 54√3 =
Объяснение:
1)По какой формуле находят длину окружности?
С=2πR
2)Как обозначается отношение длины окружности к ее диаметру?
π
3) По какой формуле находят длину дуги окружности?
l=(π r n)/180°
4)По какой формуле находят площадь круга?
S=πR²
5)Что называется сектором?
Сектор круга — часть круга, ограниченная дугой и двумя радиусами, соединяющими концы дуги с центром круга.
6)По какой формуле находят площадь сектора?
S = (π *r² *α)/360°.
7)Что называется кругом?
Круг - часть плоскости, лежащая внутри окружности.