Объяснение:
1)
Дано
Правильная пирамида
Основание квадрат
а=6 ед. сторона квадрата
b=5 ед. ребро пирамиды
Sпол.=?
Решение
Sпол.=Sосн.+4Sгр.
Основание квадрат
Sосн.=а²=6²=36 см² площадь квадрата
Sгр=k*a/2 где k- апофема
k=√(b²-(a/2)²), где b- ребро пирамиды, а -сторона квадрата
k=√(25-3²)=√(25-9)=√16=4 апофема.
Sгр.=4*6/2=12 площадь грани.
Sпол.=36+4*12=36+48=84 ед²
ответ: 84
2)
Дано
Пирамида
Основание квадрат
k=10 апофема
h=8 высота.
V=?
Решение.
V=1/3*Sосн.*h
Апофема гипотенуза, высота катет, найдем второй катет.
По теореме Пифагора найдем половину стороны квадрата.
а/2=√(10²-8²)=√(100-64)=√36=6 половина стороны квадрата.
а=а/2*2=6*2=12 сторона квадрата.
Sосн=а²=12²=144
V=1/3*144*8=384
ответ:384ед.³ объем
3)
Дано
Пирамида
Основание квадрат.
b=5 ребро пирамиды
a=6 сторона квадрата.
Sбок=?
Решение.
Найдем апофему, ребро гипотенуза, а половина стороны квадрата катет, найдем второй катет.
k=√(b²-(a/2)²)=√(25-9)=√16=4 апофема.
Sгр.=k*a/2=4*3=12 площадь грани.
Sбок.=4*Sгр.=4*12=48
ответ:48 ед² площадь боковой поверхности пирамиды.
4)
Дано
Пирамида
Основание квадрат.
k=15 апофема
h=12 высота
а=?
Решение.
Апофема, высота и половина стороны квадрата, образуют прямоугольный треугольник, где апофема является гипотенузой данного треугольника.
По теореме Пифагора найдем половину стороны квадрата.
а/2=√(k²-h²)=√(15²-12²)=√(225-144)=√81=9. половина стороны квадрата.
а=а/2*2=9*2=18
ответ: сторона квадрата равная 18 ед.
ответ: Sпол=70,65см²; V=67,5√3см³.
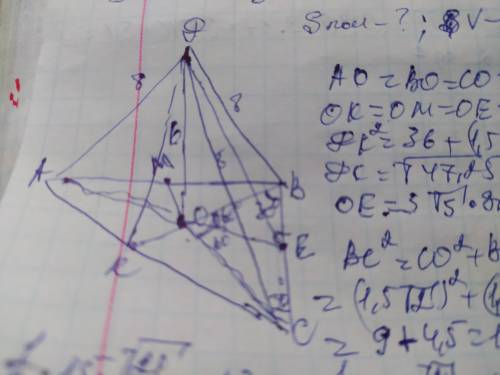
Объяснение: в основании правильной 3-угольной пирамиды лежит равносторонний треугольник поэтому все стороны основания равны. Обозначим вершины пирамиды АВСД с высотой ДО. Проведём из трёх вершин основания медианы АЕ, СМ, ВК. При пересечении они делятся в отношении 2:1, начиная от вершины угла. Рассмотрим ∆СДО. Он прямоугольный где ДО и СО- катеты, а СД- гипотенуза. Найдём СО по теореме Пифагора:
СО²=СД²-ДО²=8²-6²=64-36
СО√45=3√5см
СО=ВО=АО=3√5см
Так как медианы делятся в отношении 2:1, то МО=КО=ЕО=3√5/2=1,5√5см
Проведём апофему ДЕ. Она является гипотенузой в ∆ДЕО. Найдём апофему ДЕ по теореме Пифагора:
ДЕ²=ДО²+ЕО²=6²+(1,5√5)²=36+2,25×5=
=36+11,25=47,25; ДЕ=√47,25=15√0,21=
=15×√(21/100)=15√21/10см
Рассмотрим ∆ВОС. В нём известны 2 стороны и угол между ними. Найдём сторону основания ВС по теореме синусов:
ВС²=ВО²+СО²-2×ВО×СО×cos120°=
=(3√5)²+(3√5)²-2×3√5×3√5×(-½)=
=9×5+9×5-9×5=135; BC=√135=3√15см
Найдём площадь боковой грани пирамиды зная её высоту и сторону основания по формуле: Sбок.гр.=½×BC×ДЕ=
=½×3√15×15√21/10=9√315/4=3√35/4см²
Так как таких граней 3 то:
Sбок.пов=3√35/4×3=9√35/4см²
√35≈5,9;. √3≈1,7
Теперь найдём площадь основания по формуле:
Sосн=a²√3/4=(3√15)²√3/4=9×15√3/4=
=135√3/4см²
Sпол=Sосн+Sбок.пов=135√3/4+9√35/4=
=33,75×1,7+2,25×5,9=57,375+13,275=
=70,65см²
Теперь найдём объем пирамиды зная площадь основания и высоту по формуле:
V=⅓×Sосн×ДО=⅓×135√3/4×6=67,5√3см³.