1) Если внешний угол при вершине В равен 111градусов, то внутренний как смежный угол равен 180-111=69 град. Т.к. треугольник равнобедренный, то углы В и А равны. Следовательно, если сумма всех углов треугольника равна 180градусов, угол при вершине С = 180 - (69+69) = 42 градуса.
2) аналогично. (180-20):2= 80, т.е. по 80 градусов угол В и угол А.
3) пусть х - коэффициент пропорциональности. тогда 2х+3х+7х=180. х=15 градусов. Меньший угол тогда 2 умножить на 15 = 30градусов
4) аналогично. х+2х+4х+8х=360. х=24 грудса, т.е. меньший угол.
5) сумма углов параллелограмма = 360градусов. т.к. диагональ разделяет угол при вершине параллелограмма на 2 части, то этот угол будет равен 61+47 = 108градусов.Другой угол параллелограмма будет равен = (360 - (2·108))÷2 = 73 градуса
6) пусть меньшее основание х, тогда большее равно х+16. По свойству средней линии трапеции: 2·18 = х + (х+16), отсюда х = 10. ответ: 10.
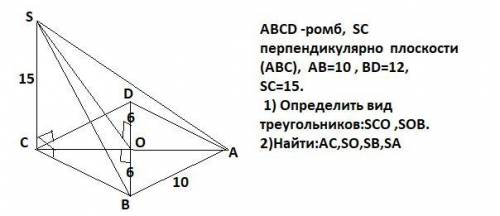
ABCD -ромб, SC перпендикулярно плоскости (АВС), АВ=10 , ВD=12, SC=15. 1) Определить вид треугольников:SCO ,SOB. 2)Найти:AC,SO,SB,SA
Объяснение:
1) Т.к. SC ⊥ (АВС), то SC перпендикулярна любой прямой , лежащей в этой плоскости ⇒ SC ⊥ СО , поэтому ΔSCO- прямоугольный.
По свойству диагоналей ромба СА⊥BD . Тогда по т. о трех перпендикулярах : если проекция СО⊥ОВ ( прямой , лежащей в плоскости), то и наклонная SO⊥OB ⇒ΔSOB -прямоугольный.
2)По свойству диагоналей ромба : ∠ВОА=90° и ВО=12:2=6
ΔВОА прямоугольный , по т. Пифагора ОА=√(10²-6²)=8 ⇒ АС=2*8=16 .
ΔSCO-прямоугольный ,CO=OA=8 , по т. Пифагора SO=√(15²+8²)=17 .
ΔSOB-прямоугольный ,по т. Пифагора SB=√(17²+6²)=√325=5√13 .
ΔSCA-прямоугольный ,по т. Пифагора SB=√(15²+16²)=√481.
В ∆ АЕ1В и ∆ АЕ2В две стороны равны ( по условию), сторона АВ - общая.
∆ АЕ1В = ∆ АЕ2В по 3-му признаку равенства треугольников. ⇒
∠Е1ВА=∠Е2ВА , ⇒ смежные им ∠Е1ВD =∠Е2ВD.
В ∆ Е1ВD и Е2ВD стороны Е1В=Е2В, сторона ВD - общая, углы между этими сторонами равны. ⇒
∆ Е1ВD =∆ Е2ВD по 1-му признаку равенства.⇒ DE1=DE2
В ∆ CDE1 и ∆ CDE2 стороны Е1D=Е2D, сторона СD общая, равенство углов между ними следует из доказанного выше ∆ Е1ВD =∆ Е2ВD ⇒
∆ CDE1=∆ CDE2 по 1-му признаку равенства, ч.т.д.