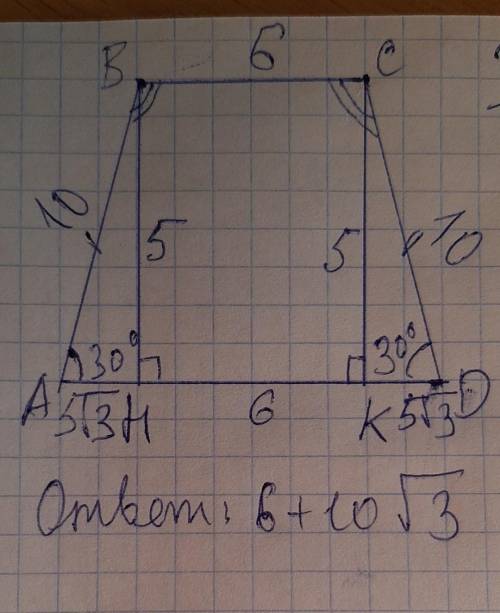
Решение: Проведём высоту СК.
Значит, BHKC прямоугольник, тогда ВС=HK=6 , BH=CK=5.
В треугольнике АВН угол АНВ= 90°, значит треугольник АВН - прямоугольный, т.к. угол А=30° и катет ВН=5, то гипотенуза АВ= 10 ( т.к. в прямоугольном треугольнике катет лежащий против угла в 30° равен половине гипотенузы).
Т.к. АВСD - равнобедеренная трапеция, то угол А = углу D = 30°.
Значит треугольник АВН= треугольнику СКD (по гипотенузе и острому углу)
Треугольнике АВН - прямоуольный:
По теореме Пифагора:
АН² + ВН²= АВ²
АН² = АВ² - ВН²
АН² = 100 - 25 = 75
АН = корень в квадрате из 75 = 5 корней из трёх
АН = КD = 5 корней из трёх
АD = 6 + 5 корней из трёз + 5 корней из трёх = 6 + 10 корней из трёх.
ответ: 6 + 10 корней из трёх.
АВ= 20 м, АО=16 м, ВО= 20м. Решим по теореме косинусов.
АВ²=АО²+ВО²-2*АО*ВО*cosO.
cosO=(AO²+BO²-AB²) / (2*AO*BO) = (256+400-400)/(2*16*20) =0,4
Из треугольника ВОС найдем сторону ВС, косинус угла ВОС будет -0,4.
ВС²=ВО²+СО²-2*ВО*СО*cos(BOC)=400+256-2*20*16*(-0,4)=912.
ВС=√912.