Обратим внимание на то, что речь идет о противоположных углах, а не об углах, прилежащих к одной боковой стороне трапеции. Основания трапеции параллельны, каждая боковая сторона при них - секущая. Поэтому сумма углов, прилежащих к одной боковой стороне трапеции, равна 180°, так как они внутренние односторонние при пересечении параллельных прямых секущей.
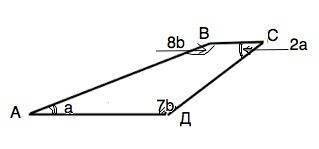
Обозначим трапецию АВСД. По условию ∠А:∠С=1:2
∠Д:∠В=7:8
Примем угол А=а, тогда угол С=2а.
Примем угол Д=7b, тогда угол В=8b
a+8b=180°
2a+7b=180°
Приравняем левые части уравнений:
а+8b=2a+7b⇒
b=a
Подставим в первое уравнение вместо b – а, т.к. они равны.
Тогда а+8а=180°⇒
а=20° и b=20°.
Следовательно, ∠ВАД=20°, ∠АВС=8•20°=160°;
∠ВСД=2•20=40°; ∠СДА=7•20=140°.
Основания трапеции параллельны, каждая боковая сторона при них - секущая. Поэтому сумма углов, прилежащих к одной боковой стороне трапеции, равна 180°, так как они внутренние односторонние.
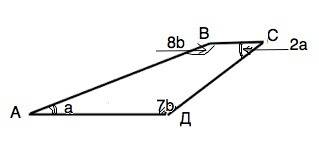
Обозначим трапецию АВСД. По условию ∠А:∠С=1:2
∠Д:∠В=7:8
Примем угол А=а, тогда угол С=2а.
Примем угол Д=7b, тогда угол В=8b
a+8b=180°
2a+7b=180°
Приравняем левые части уравнений:
а+8b=2a+7b⇒
b=a
Подставим в первое уравнение вместо b - а
Тогда а+8а=180°⇒
а=20°. Следовательно, ∠ВАД=20°, ∠АВС=8•20°=160°;
∠ВСД=2•20=40°; ∠СДА=7•20=140°.
Значит, F₁P₁ и F₂P₂ параллельны и лежат в одной плоскости с точкой О.
Рассмотрим треугольники ОF₁P₁ и ОF₂P₂:
угол при вершине О - общий;
∠ОF₁P₁ = ∠ОF₂P₂ как соответственные при пересечении параллельных прямых F₁P₁ и F₂P₂ секущей OF, значит
ΔОF₁P₁ подобен ΔОF₂P₂ по двум углам.
ОP₁ : ОР₂ = F₁P₁ : F₂P₂
ОP₁ = х, ОP₂ = х + 4
x : (x + 4) = 3 : 5
5x = 3(x + 4)
5x = 3x + 12
2x = 12
x = 6
ОP₁ = 6 см