Объяснение:
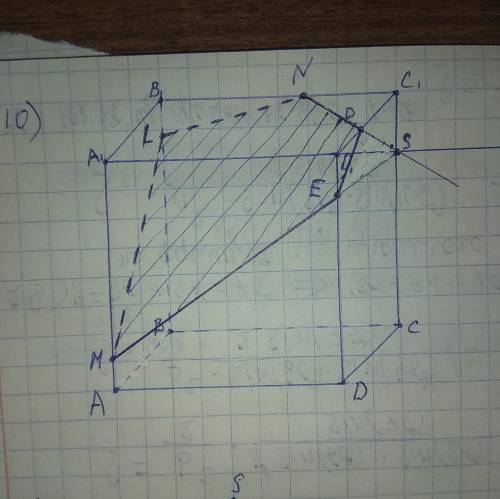
10) Здесь можем провести прямую через точки N и P, лежащие в одной плоскости (A1B1C1). Ее след — NP (видимый). Больше нет точек, лежащих в одной плоскости либо в параллельных плоскостях.
Продолжим прямую NP. Она лежит в плоскости (A1B1C1), поэтому пересечься может только с одной из прямых этой плоскости. С A1D1 и C1D1 точки пересечения уже есть — N и P. Еще две прямые этой плоскости — C1D1 и A1D1 . Точка пересечения A1D1 и NP — S. Поскольку она лежит на прямой A1B1, то принадлежит плоскости ( DCC1), а значит, через нее и точку M, лежащую в этой же плоскости, можно провести прямую. Прямая MS пересекает ребро DD1 в точке E. ME — ее след (видимый). Через точки P и E, лежащие в одной плоскости (DCC1), можно провести прямую, след которой — PE (видимый). В плоскости (DCC1) есть прямая PE, в параллельной ей плоскости (ABB1) — точка M. Через точку M можем провести прямую ML, параллельную PE. Она пересекает ребро BB1 в точке L. ML — след этой прямой (невидимый). Точки N и L лежат в одной плоскости (BCC1), значит, через них можно провести прямую. Ее след — NL (невидимый). Пятиугольник MLNPE — искомое сечение.
3) Здесь точки M и N лежат в одной плоскости ABS, соединяем их, получившийся след MN (видимый). Точки M и P лежат в одной плоскости APS, соединяем их, получаем прямую, след которой MP (невидимый). Точки N и P лежат в одной плоскости ABP, соединяем их, получаем прямую, след которой NP (невидимый). Треугольник NPM - искомое сечение.
Всё просто))) Надеюсь понятно объяснил

Объяснение:
один из углов треугольника равен 2х, то второй=3х, а третий=4х.
Т.к. сумма углов треугольника=180 гр., то
2х+3х+4х=180
9х=180
х=20 (градусам)
Тогда,
1) первый угол = 2*20=40(гр.), а его внешний угол будет равным 180-40=140(гр)
2) второй угол=3*20=60 (гр.), а его внешний угол будет равным 180-60=120(гр)
3) третий угол=4*20=80(гр),, а его внешний угол будет равным 180-80=100(гр)
Следовательно внешние углы будут относится, как 140:120:100,
сокращая на 20 получим, что внешние углы треугольника относятся, как 7:6:5