1). S1/S2 = (r/R)^2
В правильном шестиугольнике сторона равна радиусу опис. окр -ти, а радиус r впис. окружности(высота, опущенная на сторону) равен (Rкор3)/2.
S1/S2 = 3/4.
2)Распишем площадь тр-ка А1А4А5:
S1 = (1/2)*А1А5 * А1А4* sin(45/2), т.к. угол А4А1А5 = А4ОА5/2 = (360/8)/2 = 45/2.
А1А5 = 2R -большая диагональ 8-гольника равна диаметру описанной окр-ти.
А1А4 = 2R*cos(45/2)
Выражаем площадь:
S1 = (1/2)*2R*2Rcos(45/2)*sin(45/2) = R^2 *sin45 = (R^2кор2)/2 ;
Но по условию она равна 8кор2.
(R^2кор2)/2 = 8кор2.
Отсюда R = 4
Теперь переходим к тр-ку А1А4А6:
S = (1/2)(A1A4)^2 *sin45 ,т.к. А1А4 = А1А6 = 2Rcos(45/2)
Найдем cos(45/2) = кор((1+cos45)/2) = (кор(2+кор2))/2
S = (1/2) R^2*(2+кор2)*(кор2)/2 = 8(1+кор2)
((кор2)-1)S = 8
ответ: 8.
3) Это прямоугольник, так как углы его опираются на главные диагонали - диаметр описанной окружности.S = a*A1A6 = (2Rsin(45/2))*(2Rsin(135/2) = (2Rsin(45/2)*(2Rcos(45/2)) = 2R^2 sin45 = R^2 *кор2.
Найдем R^2:
А4А6 = 2Rsin45 = Rкор2
А4А6^2 = 2R^2 = 289кор2
R^2 = (289кор2)/2.
Теперь находим площадь:
S = R^2 кор2 = 289
ответ: 289
1) Треугольники вне восьмиугольника равны по двум сторонам и углу между ними(по свойству правильного многоугольника), значит стороны вписанного многоугольника равны, а т.к. его стороны равны, то это правильный восьмиугольник.
2)В треугольнике АВМ:АД-высота(т.к.угол АДМ=90), также АД является медианой этого треугольника(ВД=МД по условию) из этого следует, что треугольник АВМ-равнобедренный. Тогда АВ=АМ=4. И т.к. АМ=МС, АС=АМ+МС=4+4=8.
3)Треугольники вне восьмиугольника равны по двум сторонам и углу между ними(по свойству правильного многоугольника), значит стороны вписанного четырехугольника равны, и это значит, что это четырехугольник-ромб, т.к. диагонали правильного восьмиугольника равны, то и в ромбе диагонали равны, из чего следует, что это квадрат.
4)Обозначим СД=х.Проведем высоты ВН1 и СН2, угол ДСН2=90-60=30. Тогда ДН2=1/2 СД=х/2. Т.к. АД=2х, то АН1=2х-х-х/2=х/2, из этого следует, что трапеция равнобедренная, а значит СД=2. Тогда АД=2СД=2*2=4. СН2=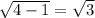
. S=СН2*АД=корень из 3*4=4 корня из 3
Из точки К опустим перпендикуляр на АВ в точку К1, это проекция точки К на плоскость основания. Из точки К1 параллельно АС проведём прямую К1М1 до пересечения с ВС в точке М1. Из точки М1 восстановим перпендикуляр М1М к плоскости верхней грани куба до пересечения с В1С1 в точке М. Соедини Ки М. КМ будет параллельна АС поскольу грани куба параллельны и КК1 и ММ1 перпендикуляры к этим граням. Полученное сечение это равнобедренная трапеция АКМС. Известно что АС=а корней из 2=4 корня из2., аналогично КМ=2 корня из 2. Проведём в трапеции АКМС высоту КЕ к АС. АЕ=(АС-КМ)/2=((4корня из 2)/2-(2корня из 2)/2):2=корень из 2.АК=корень из(А1К квадрат+АА1квадрат=корень из 20. Тогда высота трапеции КЕ=корень из (АКквадрат-АЕ квадрат)= корень из(20-2)=3 корня из 2. Отсюда площадь сечения S=1/2(КМ+АС)*КЕ=((2 корня из 2)+(4 корня из 2)):2*(3 корня из 2)=18.