Дан усеченный конус радиуса 3 см и 12 см. высота равна 12 см найти sполон.

👇

Ответ:

messaivi

11.10.2020

Площадь большего основания
S₁ = π·r₁² = π·12² = 144π
Площадь меньшего основания
S₂ = π·r₂² = π·3² = 9π
Разность радиусов составляет 12-3 = 9 см
Образующую конуса a найдём по теореме Пифагора
a² = (r₁-r₂)²+h²
a² = 9²+12²=81+144 = 225
a = √225 = 15 см
Площадь боковой поверхности усечённого конуса
S₃ = π·(r₁+r₂)·a = π·(12+3)·15 = 225π
И полная площадь
S = S₁+S₂+S₃ = 144π+9π+225π = 378π ≈ 1187.52 см²

4,6(50 оценок)

Открыть все ответы

Ответ:

vitaly1552

11.10.2020

во втором у меня получается не 5 $\sqrt{3}$ , a 3 $\sqrt{3}$

2. Т.к. ADM - внешний угол, он равен сумме не смежных с ним углов, т.е. он равен ACD+CAD, т.к угол ACD=30градусов, то и угол CAD = 30 градусов, а значит треугольник ADC равнобедренный, AD=CD=3см и угол ADC=120градусов

по теореме синусов находи неизвестную сторону:

AD/sin30= CD/sin30= AC/sin120

6 = 6 = AC /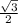 $\frac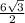{\sqrt{3}}{2}$

AC= $\frac{6\sqrt{3}}{2}$ =3 $\sqrt{3}$

3. в параллелограмме диагонали точкой пересечения делятся пополам.

AP=OC, BO=OD. угол СОД=60 градусам

Применяем теорему косинусов:

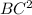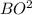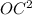$BC^{2}$ = $BO^{2}$ + $OC^{2}$ -2BC*OC*cos120

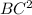$BC^{2}$ = 9+25-2*3*5*(-1/2)= $\sqrt{49}$ =7

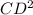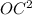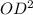$CD^{2}$ = $OC^{2}$ + $OD^{2}$ -2OC*OD*cos60

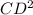$CD^{2}$ = 9+25-2*3*5*(1/2)= $\sqrt{19}$

периметр параллелограмма = 7+7+ $\sqrt{19}$ + $\sqrt{19}$ = 14+2* $\sqrt{19}$

точки A,D,M лежат наодной прямой, угол ADM= углу BCD, т.к. это соответственные углы при параллельных прямых и секущей.

через теорему косинусов находим BD:

$BD^{2}$ = 9+25-2*3*5*(1/2)=34-15=19

BD= $\sqrt{19}$

4,5(46 оценок)

Ответ:

Tigr111111112

11.10.2020

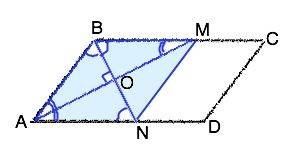
ВС|║АD, АВ - секущая. ⇒ сумма внутренних односторонних углов равна 180°. Биссектрисы делят углы пополам.⇒ из суммы углов треугольника угол ВОА=180°- 0,5•(∠АВС+∠ BAD)=90°,

Биссектриса угла параллелограмма отсекает от него равнобедренный треугольник ( для доказательства рассмотри накрестлежащие углы при секущих ВN и АМ) ⇒ ВМ=АВ, АN=AB ⇒ ВМ=АN. В ∆ ВМN отрезок ВО=ОN (т.к.в ∆ АВМ АО - медиана),⇒ МО - медиана и высота ( угол ВОМ =90° как смежный углу ВОА) ⇒ треугольник ВМN – равнобедренный и МN =ВМ Противоположные стороны четырехугольника АВMN равны и параллельны ( лежат на параллельных прямых), следовательно, АВMN– параллелограмм по определению. Кроме того, этот четырехугольник - ромб, т.к. все его стороны равны, а диагонали взаимно перпендикуляры и являются биссектрисами его углов. .