Объяснение:
Все грани прямоугольного параллелепипеда - прямоугольники.
ΔА₁АС: ∠A₁AC = 90°
sinβ = AA₁ / A₁C, ⇒ AA₁ = A₁C · sinβ,
AA₁ = a · sinβ
cosβ = AC / A₁C, ⇒ AC = A₁C · cosβ,
AC = a · cosβ.
Точка пересечения диагоналей прямоугольника является центром описанной окружности. Тогда для окружности, описанной около прямоугольника ABCD ∠АОВ - центральный, а ∠ACB - вписанный, опирающийся на ту же дугу, значит
∠АCB = 1/2 ∠AOB = α/2.
ΔABC: ∠ABC = 90°
sin∠ACB = AB / AC, ⇒ AB = AC · sin∠ACB,
AB = a · cosβ · sin(α/2),
cos∠ACB = BC / AC, ⇒ BC = AC · cos∠ACB,
BC = a · cosβ · cos(α/2).
Sбок = Pосн · AA₁
Sбок = (AB + BC) · 2 · AA₁
Sбок = (a · cosβ · sin(α/2) + a · cosβ · cos(α/2)) · 2 · a · sinβ =
= a · cosβ(sin(α/2) + cos(α/2)) · 2 · a · sinβ =
= 2a²sinβ·cosβ(sin(α/2) + cos(α/2)) =
= a²sin2β (sin(α/2) + cos(α/2))
Ці точки лежать на серединному перпендикулярі точок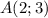 
та 
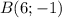. Знайдемо координати точки 
— середини відрізка 
:
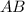Щоб знайти кутовий коефицієнт серединного перпендикуляра, знайдемо кутовий коефіцієнт прямої :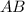
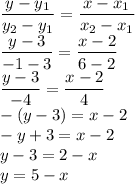
Коефіцієнт перпендикулярної прямої дорівнює 
. Застосуємо формулу прямої за кутовим коефицієнтом і точкою, через яку пряма проходить:
Тобто серединний перпендикуляр має формулу 
.
Знайдемо точку його перетину:
а) З віссю абсцисс:
Тобто точка має координати (3; 0).
б) З віссю ординат:
Все зобразив на графіку. Перемалюйте його в зошит, щоб отримати вищу оцінку ;)
Відповідь:
а) (3; 0)
б) (0; –3)
175:35÷5- в 5 раз площадь второго треугольника больше площади первого
Если площади больше, значит и стороны тоже, следовательно:
4×5=20см
14×5=70см
17×5=85см
ответ:20см, 70см, 85см