У нас есть равнобедренная трапеция ABCD, у которой углы BAD и CDA острые и равны 45 градусов (угла равны, т.к. трапеция равнобедренная). Из точки В проведем высоту ВМ, угол ВМА равен 90 градусов, следовательно, угол МВА=45 градусов. поскольку угол МВА=ВАМ=45, то треугольник ВМА равнобедренный, а значит стороны ВМ и МА равны. проведем из С высоту СК, тогда у нас получится прямоугольник ВМКА, у которого стороны ВС=МК=6, трегольники АВМ и СDК равны, следовательно, стороны АМ и КD также равны, АМ=DK=(8-6)/2=1
площадб трапеции находится по формуле (a+b)/2*h, подставим в эту формулу то, что мы знаем и получим конечную формулу Sabcd=(6+8)/2*1=7
Пусть х м - длина основания равнобедренного треугольника, где x>0, тогда длина боковой стороны этого же равнобедренного треугольника по условию равна 12х м, т.к. периметр этого треугольника равен 10 м по условию, получаем уравнение:
х+12х+12х=10
25х=10
х=0,4
Значит, 0,4 м - длина основания.
ответ: 0,4 м.
Теорема Пифагора: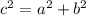 
, где с - гипотенуза, а а и b - катеты прямоугольного треугольника.
К равнобедренному треугольнику она не относится (исключение составляет если основание равнобедренного треугольника является гипотенузой прямоугольного треугольника, т.е. угол, лежащий против основания равнобедренного треугольника - прямой, т.е. равен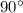 
).
Формально, если прямая задана уравнением, то если подставить в него координаты точки, то знак выражения, которое получится, определяет полуплоскость. Если, подставляя одну точку, получаем выражение одного знака, а подставляя вторую - другого, то эти точки лежат в разных полуплоскостях