Найдем другой угол параллелограмма зная, что сумма смежных (соседних) углов параллелограмма равна 180°:
180° -60° = 120°
Рассмотрим треугольники образованные боковыми сторонами и диагоналями.
Треугольник со сторонами 12 и 20 см и углом между ними 60°: третья сторона d1 будет диагональю параллелограмма.
Используем теорему косинусов ("Квадрат стороны треугольника равняется сумме квадратов 2-х других сторон минус удвоенное произведение этих сторон на косинус угла между ними"):
d1 = √(12²+20²-2*12*20*cos60°) = √(144+400-480*0.5) = √304=√(16*19)=4√19
Треугольник со сторонами 12 и 20 см и углом между ними 120°: третья сторона d2 будет диагональю параллелограмма.
d2 = √(12²+20²-2*12*20*cos120°) = √(144+400+480*0.5) = √784 = 28
Объяснение:
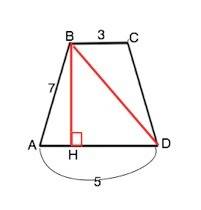
Проведем высоту ВН к большему основанию.
Высота равнобедренного треугольника, проведенная к большему основанию, делит его на отрезки, меньший из которых равен полуразности оснований, больший - их полусумме.
АН=(AD-BC):2=1
HD=(BC+AD):2=4
Из прямоугольного ∆ АВН по т.Пифагора высота
ВН=√(AB²-AH²)=√48=4√3
Из прямоугольного ∆ DBH диагональ
ВD=√(BH²+HD²)=√(48+16)=8 см (диагонали равнобедренной трапеции равны, ⇒ АС=8 см)
Площадь трапеции равна произведению высоты на полусумму оснований.
S=4√3•4=16√3 см*
ЕF=2ЕМ=24*2=48 см.
ответ: 48 см.