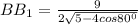
ответ:Геометрический смысл φ ясен из рис. 125. Отрезок прямой разделен на два отрезка А и В, которые, как говорят, образуют "золотое сечение" отрезка А + В: длина всего отрезка (А + В) находится в таком же отношении к длине отрезка А, как и длина отрезка А к длине отрезка В. Отношение каждой пары отрезков и равно числу φ. Если длина отрезка В равна 1, то значение φ нетрудно вычислить из уравнения
которое можно записать в виде обычного квадратного уравнения А2 - А - 1 = 0. Положительный корень этого уравнения равен
Это число одновременно выражает длину отрезка А и значение величины φ. Его десятичное разложение имеет вид 1,61803398... Если за единицу принять длину А, то длина В будет выражаться величиной, обратной φ, то есть 1/φ. Любопытно, что 1/φ = 0,61803398... Число φ - единственное положительное число, которое переходит в обратное ему при вычитании единицы.
Подобно числу π, φ можно представить в виде суммы бесконечного ряда многими Предельная простота следующих двух примеров еще раз подчеркивает фундаментальный характер φ:
В треугольнике АВТ ВО - биссектриса и высота, значит ΔАВТ равнобедренный, АВ = ВТ = ВС/2 (Т - середина ВС по условию), а так как ВО еще и медиана, то АО = ОТ = АТ/2 = 5.
По свойству биссектрисы треугольника AQ : QC = AB : BC = 1 : 2, тогда
CQ : CA = 2 : 3.
Проведем QS║AT.
ΔCQS подобен ΔCAT по двум углам (угол при вершине С общий, ∠CQS = ∠CAT как соответственные при QS║AT и секущей АС), ⇒
QS : AT = CQ : CA = 2 : 3
QS = 2AT / 3 = 20/3
ΔВОТ подобен ΔBQS по двум углам (угол при вершине В общий, ∠BOT = ∠BQS как соответственные при QS║AT и секущей BQ), ⇒
BO : BQ = OT : QS
BO : 16 = 5 : (20/3)
BO = 16 · 5 / (20/3) = 80 · 3 / 20 = 12 ⇒ OT = BT - BO = 16 - 12 = 4
ΔBOT: по теореме Пифагора
ВТ = √(ВО²+ ОТ²) = √(144 + 25) = 13 ⇒
АВ = 13, ВС = 26.
ΔAOQ: по теореме Пифагора
AQ = √(AO² + OQ²) = √(25 + 16) = √41
AC = 3AQ = 3√41