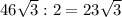 ,
, = 23 * 3 = 69
= 23 * 3 = 69В прямоугольнике диагонали равны и точкой пересечения делятся пополам и тем самым образуют две пары равнобедренных треугольников. Пусть точка O - точка пересечения диагоналей. Рассмотрим треугольник AOB - равнобедренный, углы при основании равны. Можем определить угол при вершине этого равнобедренного треугольника, он же будет одним из углов между диагоналями.
Угол AOB = 180° - (42° + 42°) = 96°.
Это и будет больший угол, т.к. смежный с ним угол AOD = 180° - 96° = 84°.
ответ: больший угол равен 96°.
ΔАКД=ΔКДС по первому признаку. В равных треугольниках против равных углов лежат равные стороны⇒АД=ДС и ΔАДС-равнобедренный, что и требовалось доказать.
Другое решение:
ДК- медиана и высота ΔАСД, а это является свойством равнобедренных треугольников. В равнобедренном треугольнике: высота и медиана, исходящие из угла, образованного равными сторонами, один и тот же отрезок⇒АД=ДС и ΔАДС-равнобедренный.