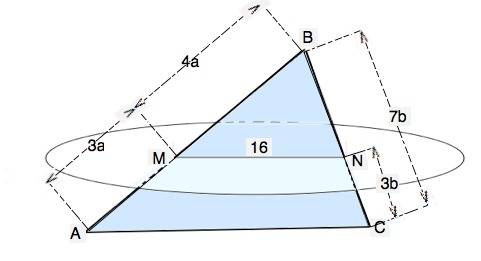
Примем коэффициент отношения отрезков на АВ равным а,Так как AM : MB = 3:4, то АВ=АМ+ВМ=7а ⇒ AM:AB = 3:7.
CN:CB = 3:7- дано.
а) Точки М и N лежат в плоскости ∆ АВС и в плоскости α. ⇒MN - линия пересечения этих плоскостей.
МN и АС высекают на прямых АВ и ВС пропорциональные отрезки.
Из обобщённой теоремы Фалеса: если отрезки, высекаемые прямыми на одной прямой, пропорциональны отрезкам, высекаемым теми же прямыми на другой прямой, то эти прямые параллельны.⇒ АС║MN.
Если прямая (АС), не лежащая в плоскости α, параллельна некоторой прямой (MN), которая лежит в плоскости α, то прямая параллельна плоскости . ⇒АС || α
б) Т.к. MN║AC, углы при их пересечении секущими АВ с одной стороны и ВС с другой равны как соответственные. Отсюда следует подобие треугольников MBN и ABC с коэффициентом подобия k=BC:NC=7:3 ⇒ AC:MN=7:3
AC:16=7:3––АС=16•7:3=28 см
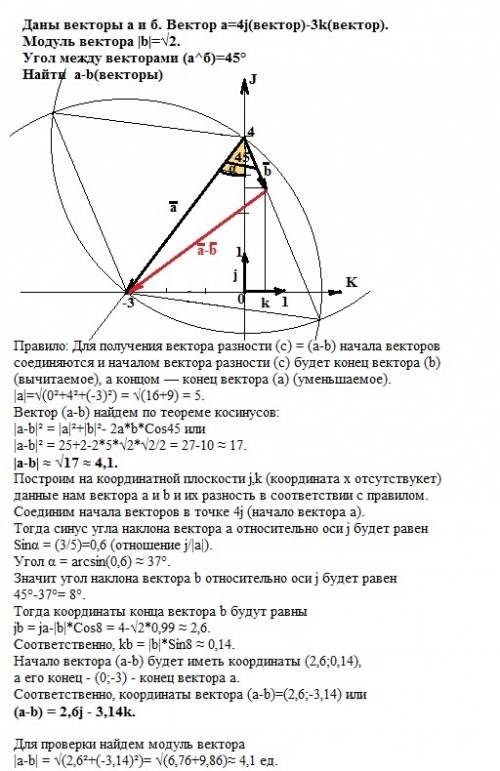
Правило: Для получения вектора разности (c) = (a-b) начала векторов соединяются и началом вектора разности (c) будет конец вектора (b) (вычитаемое), а концом — конец вектора (a) (уменьшаемое).
Решение.
Для начала найдем модуль вектора а.
Дано разложение вектора по ортам: a=4i-3k, то есть координаты вектора
равны:
X=0 (так как базовый вектор i отсутствует),
Y=4 и Z=-3.
То есть дан вектор а(0;4;-3).
Тогда его модуль равен:
|a|=√(0²+4²+(-3)²) = √(16+9) = 5.
Вектор (a-b) найдем по теореме косинусов:
|a-b|² = |a|²+|b|²- 2a*b*Cos45 или
|a-b|² = 25+2-2*5*√2*√2/2 = 27-10 ≈ 17.
|a-b| ≈ √17 ≈ 4,1.
Мы нашли модуль (длину) вектора разности векторов а и b.
Но можно найти и его разложение по базовым векторам.
Для этого необходимо найти координаты конца вектора b
относительно начала координат.
Построим на координатной плоскости j,k (координата х отсутствукет)
данные нам вектора а и b и их разность в соответствии с правилом.
Соединим начала векторов в точке 4j (начало вектора а).
Тогда синус угла наклона вектора а относительно оси j будет равен
Sinα = (3/5)=0,6 (отношение j/|a|).
Угол α = arcsin(0,6) ≈ 37°.
Значит угол наклона вектора b относительно оси j будет равен
45°-37°= 8°.
Тогда координаты конца вектора b будут равны
jb = ja-|b|*Cos8 = 4-√2*0,99 ≈ 2,6.
Соответственно, kb = |b|*Sin8 ≈ 0,14.
Начало вектора (a-b) будет иметь координаты (2,6;0,14)
а его конец - (0;-3) - конец вектора а.
Соответственно, координаты вектора (a-b)=(2,6;-3,14) или
(a-b) = 2,6j - 3,14k.
Для проверки найдем модуль вектора
|a-b| = √(2,6²+(-3,14)²)= √(6,76+9,86)≈ 4,1 ед.
Это соответствует ранее найденному значению с учетом округлений.
Обозначим a - меньший угол параллелограмма, лежащнго в основании, д1 - длину большой диагонали паралелограмма, лежащего в основании паралллелепипеда, д2 - длину малой диагонали паралелограмма, лежащего в основании паралллелепипеда, Д1 = 7 - большую диагональ параллелепипеда, Д2 = 5 меньшую диагональ параллелепипеда, Н - высоту параллелепипеда, sqrt - корень квадратный.
По теореме Пифагора:
H^2 + д1^2 = Д1^2 (1)
и
H^2 + д2^2 = Д2^2 (2)
По теореме косинусов:
д1^2 = 3^2 + 4^2 -2*3*4*cos a (3)
д2^2 = 3^2 + 4^2 + 2*3*4*cos a (4)
Подставим (3) и (4) в (1) и (2)
H^2 + 3^2 + 4^2 -2*3*4*cos a = 25 (5)
H^2 + 3^2 + 4^2 + 2*3*4*cos a = 49 (6)
Сложим (5) и (6)
2(H^2 +3^2 + 4^2) = 74
H^2 +9 + 16 = 37
H^2 = 12
Н = 2sqrt (3)
Вычтем (5) из (6)
2 * 2*3*4*cos a = 24
2 *24*cos a = 24
cos a =0,5
а = 60гр.
sin 60р = 0,5sqrt(3)
Площадь основания S = 3 *4 * sin 60 = 12 *0.5 sqrt(3) = 6sqrt(3)
Объём параллелепипеда V = S *H = 6sqrt(3) * 2sqrt (3) = 12 * 3 = 36