Единичный тетраэдр - треугольная пирамида, длина каждого ребра которой равна единице. Следовательно, пирамида МАВС - правильная, все ее грани - правильные треугольники.
Данное сечение - треугольник, высота которого равна высоте МО пирамиды, а основание - высоте АН основания пирамиды.
Основание О высоты правильной пирамиды - точка пересечения высот ( медиан, биссектрис) основания АВС.
АО=радиусу описанной окружности.
АО=R=a/√3=1/√3 (по формуле радиуса описанной окружности).
По т.Пифагора из ∆ АМО высота
МО=√(AM²-AO²)=√(1-1/3)=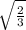
S ∆ MAH= MO•AH:2 =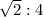
опускаем высоту...она делит треугольника АВС на 2 треугольника...АВД и АДС...из АВД найдем через теорему пифагора сторону ВД = 16 см..
так как H(квадрат) = проекция большего катета * на проекцию меньшего катета получим что ...Hквадрат = 16* у где 16 -проекция б.катета, а у - меньшего катета
отсюда 144 = 16*у, у = 9 см...гипотенуза треугольника АВС = 25 см..(16+9)
через теорему пифагора найдем сторону АС , она равна : АС (квадрат) = 625 - 400 = 225 = 15 см..
COS C = 15/25 = 3/5 = 0.6
или SIN C = 20/25 = 4/5 = 0.8