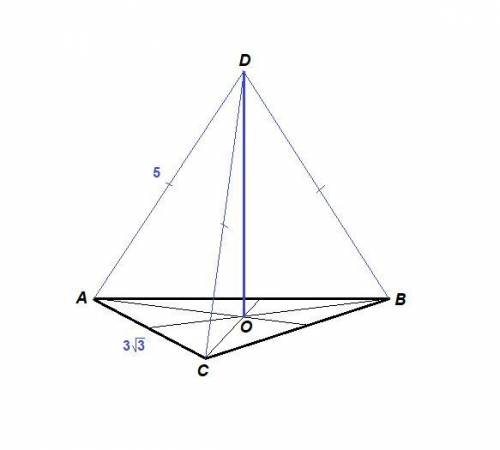
Расстояние от точки D до каждой из вершин равностороннего треугольника ABC равно 5 см, AB = 3√3 см.
Найдите расстояние от точки D до плоскости ABC.
4 см
Объяснение:
Проведем DO⊥(АВС). Тогда
DO - искомое расстояние от точки D до плоскости (ABC).
ΔDAO = ΔDBO = ΔDCO по гипотенузе и катету (DA = DB = DC по условию, DO - общий катет), тогда
АО = ВО = СО, то есть, точка О равноудалена от вершин треугольника АВС, значит О - центр описанной окружности.
Радиус окружности, описанной около правильного треугольника:
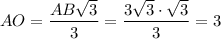 см
см
ΔDAO: ∠DOA = 90°, по теореме Пифагора
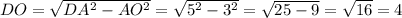 см
см
ответ: 24
Объяснение:
ΔАВН: ∠АНВ = 90°, по теореме Пифагора
АН = √(АВ² - ВН²) = √(15² - 9²) = √(225 - 81) = √144 = 12
Высота равнобедренного треугольника, проведенная к основанию, является медианой, значит
АС = 2 · АН = 2 · 12 = 24