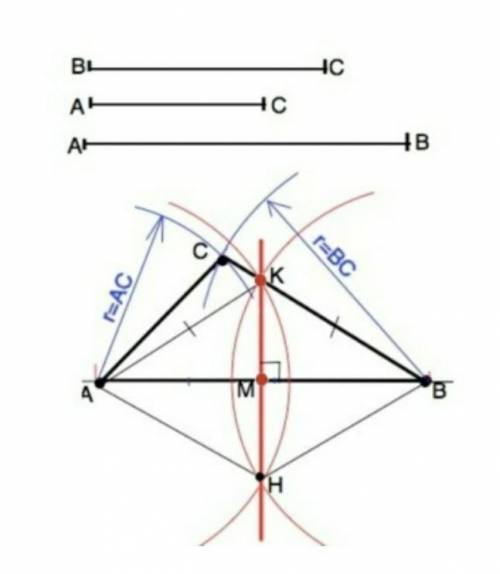
1). На произвольной прямой отложить отрезок, равный стороне АВ. Обозначить на концах отрезка вершины треугольника: точки А и В.
2) Из точки А как из центра раствором циркуля радиусом, равным длине стороны АС, начертить дугу.
3) Из т.В как из центра раствором циркуля радиусом, равным длине стороны ВС, начертить дугу до пересечения с первой дугой.
Точка пересечения дуг – вершина С искомого треугольника. Соединив А и С, В и С, получим треугольник со сторонами заданной длины.
б) Построение срединного перпендикулярна стандартное.
Из т.А и т.В как из центров провести полуокружности произвольного, но равного радиуса несколько больше половины АВ так, чтобы они пересеклись по обе стороны от АВ (т.К и т. Н).
Точки пересечения К и Н этих полуокружностей соединить.
Соединить А и Н, В и Н. Четырехугольник АКВН - ромб ( стороны равны взятому радиусу). Диагонали ромба пересекаются под прямым углом и точкой пересечения делятся пополам. =>
АМ=МВ и КМ перпендикулярно АВ.
КМ - срединный перпендикуляр к стороне АМ.
Точно так же делят отрезок пополам.
Проводим высоты в треугольниках АК и ДК, они соединятся о дной точке К, ВС - основание одно для двух. ВК = ВС, в равнобедренном треугольнике высота=медиане, биссектрисе
ДК = корень (ВД в квадрате - ВК в квадрате )= корень (676-576) =10
АК = корень (АВ в квадрате - ВК в квадрате )= корень ( 900- 576) = 18
В треугольнике АКД угол АКД находим по теореме косинусов
АД в квадрате = ДК в квадрате + АК в квадрате - 2 х АК х ДК х cos угла АКД
(2 х корень61)в квадрате = 10 в квадрате + 18 в квадрате - 2 х 10 х 18 х cos угла АКД
244 = 100 + 324 -360 х cos угла АКД
cos угла АКД = 180/360=1/2, что соответствует углу 60 град.
AD=49,BC=36,CD=x
ΔCDM∞ΔFCB по 2-м углам
MD=49-36=13
MD:BC=CD:FC
13:36=x:FC
FC=36x/13
Квадрат расстояния от данной точки до точки касания равен произведению расстояний от этой точки до точек пересечения секущей с окружностью.
FK²=FD*FC
FK²=(FC+CD)*FC
FK²=(36x/13+x)*36x/13=49*36*x²/13²
FK=42x/13
KE=FK*cosK=FK*cosD=FK*MD/CD=42x/13*13/x=42