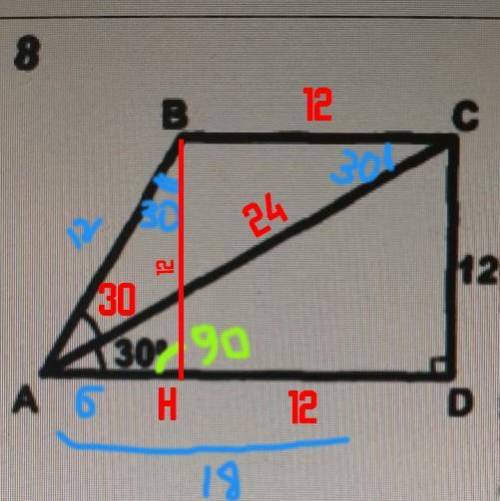
В прямоугольном треугольнике катет лежащий против угла 30 равен половине гипотенузы => AC - гипотенуза = 12 * 2 = 24.
AC - биссектриса ∠BAC = ∠CAD = 30°
∠ACD = 180° - (30° + 90°) = 60°
Т.к AC диагональ => ∠BCA = 1/2 * 60°= 30°
Проведем высоту BH => BC = HD = 12
ΔABC равнобедренный => BC = AB = 12
∠ABH = 180 - (90 + 60) = 30
В прямоугольном треугольнике катет лежащий против угла 30 равен половине гипотенузы => AH = 12 / 2 = 6.
AD = AH + HD = 6 + 12 = 18
Особенность прямоугольной трапеции в том, что её высота равна стороне, расположенной перпендикулярно двум основаниям. => BH = CD = 12
Площадь трапеции равна произведению полусуммы ее оснований на высоту
S = (a+b)/2 * h
S = (12 + 18) / 2 * 12= 180
Объяснение:
Из точки Е проведем отрезок ЕК, параллельный АВ.
Противоположные стороны параллелограмма параллельны, тоесть СВ//DE => ЕА//КВ и DE//CK
Так как в четырехугольнике КЕАВ стороны попарно параллельны, следовательно КЕАВ – параллелограмм.
ВЕ – биссектриса угла КВА по условию и диагональ параллелограмма КЕАВ.
Если диагональ параллелограмма является биссектрисой его угла, то этот параллелограмм – ромб.
Следовательно: КЕАВ – ромб
У ромба все стороны равны. Исходя из этого: ЕА=КВ=АВ=8 см.
СD=AB=8 так как противоположные стороны параллелограмма равны.
Р(АВСD)=АВ+ВС+CD+AD=AB+BK+KC+CD+DE+EA=8+8+KC+8+DE+8=32+KC+DE
Так как Р(ABCD)=46 см по условию, то получим уравнение:
32+КС+DE=46
KC+DE=14 см
Так как ЕК//АВ, а АВ//CD, то ЕК//CD;
DE//CK (доказано ранее);
Исходя из этого: CDEK – параллелограмм.
Противоположные стороны параллелограмма равны, тоесть DE=CK.
Тогда 2DE=14 см
DE=7 см
ответ: 7 см