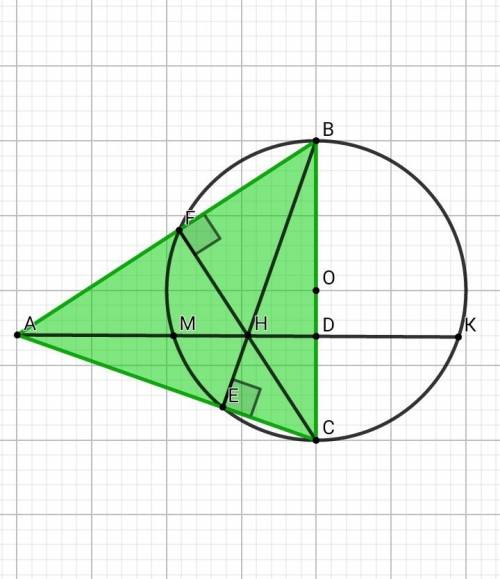
На стороне BC остроугольного треугольника ABC (AB ≠ AC) как на диаметре построена полуокружность, пересекающая высоту AD в точке M, AD = 32, MD = 8, H — точка пересечения высот треугольника ABC. Найдите AH.
Решение.
Проведём построения и введём обозначения как указано на рисунке. Угол — вписанный, опирающийся на диаметр, поэтому он равен 90°. Значит, точка пересечения прямых и — точка пересечения высот Продолжим высоту до пересечения с окружностью в точке Получаем, что По теореме о секущих получаем, что Треугольники и — прямоугольные, угол — общий, следовательно, эти треугольники подобны, откуда:
ответ: 30.
3. 14см
4. 10+2√3
Объяснение:
3. берём треугольник КLE
угол L =30°, т.к. в треугольнике 180°-90°(прямой угол)и-60°(угол К)
КЕ = 1см (как катет напротив угла 30° равен половине гипотенузы)
RS=LK =2 см (ибо параллельны)
KS=KE+ES=1+4=5
LR=KS (параллельность)
P=LR+RS+SK+KL=5+2+5+2=14cм
4. решаем по такой же схеме.
АД=ВС=3
берем треугольник АДМ(букву М я сама поставила, ибо там пусто)
треугольник АДМ равнобедренный (АД=ДМ)
по теореме косинуса:
угол А равен углу М= (180-60)/2=45°
АМ²=√АД²+ДМ²-2*АД*ДМ*соsуглаД(корень над всем)=√9+9-18*cos60°(=1/2)=√9+9-9=√9=3
АМ=√3
АВ=МВ+АМ=2+√3
ДС=АВ=2+√3(параллельность)
Р=ДС+СВ+АВ+АД=(2+√3)+3+(2+√3)+3=10+2√3