PQ = q; KP = HQ = p; пусть ∠BDC = Ф; он же равен Ф = ∠DMK = ∠FKB;
DM II AC; очевидно, что DM = q, так как EQ = q/2; -средняя линия треугольника BMD; =>
DK = q*sin(Ф); при этом DK*sin(Ф) = FK = x/2; где x = HK; искомый отрезок.
=>x/(2q) = (sin(Ф))^2;
(далее по ходу решения эту величину будет удобно принять за новую неизвестную, но к тому времени уже не важна будет её связь с углами и синусами )
Из треугольников HQL и KQL
HQ^2 - KQ^2 = HL^2 - KL^2;
HL = (x + q)/2; KL = (x - q)/2; (ну, я надеюсь, этого объяснять не надо)
KQ = KL/cos(Ф);
=> p^2 - (x/2- q/2)^2/(cos(Ф))^2 = (x/2 + q/2)^2 - (x/2 - q/2)^2 = xq;
(cos(Ф))^2 = 1 - (sin(Ф))^2 = 1 - x/(2q);
Окончательно
p^2 - (x - q)^2/(4*(1 - x/(2q))) = xq;
это уравнение уже пригодно для решения, но для упрощения я ввожу t = x/(2q); a = (p/q)^2; тогда это уравнение легко приводится к такому виду
t^2 - (1 + a)*t + a - 1/4 = 0;
Я выделю полный квадрат (чтобы не писать здоровенные корни), а потом сразу напишу ответ для x без выбора знака.
(t - (1 + a)/2)^2 = (1 + a)^2/4 - a + 1/4 = ((1 - a)^2 + 1)/4;
x = q*(1 + a +- √((1 - a)^2 + 1)); где a = (p/q)^2;
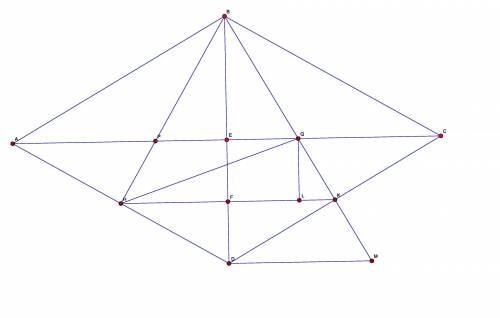
Чтобы понять, какой знак надо выбрать, я рассмотрел очевидный частный случай Ф = 60°; кстати, именно он изображен на рисунке.
В этом случае x = 3q/2; a = 7/4 (сосчитайте! надо же и вам что-то сделать :) даю подсказку - треугольники PQB и HKB равносторонние со сторонами q и x = 3q/2; соответственно, а p^2 находится из треугольника QHB по теореме косинусов), и нужным знаком оказался "минус".
Поэтому x = q*(1 + a - √((1 - a)^2 + 1)); где a = (p/q)^2;
Ну, вы сами попросили :)
11 см
Объяснение:
Перевод: Хорда круга стягивает дугу 60 градусов. Найдите длину этой хорды, если диаметр окружности равен 22 см.
Решение. Пусть хорда AB стягивает хорду 60°. Проведём из конца хорды к центру O круга отрезки AO и BO (см. рисунок). Так как проведённые отрезки равны радиусу, то
r = AO = BO = d : 2 =22 см : 2 = 11 см.
Угол α между радиусами AO и BO центральный, тогда величина угла α равна длине дуги АВ, то есть α = 60°.
Далее, длину хорды можно найти различными
Радиусы AO и BO и хорда AB образуют треугольник ABO с углом при вершине в 60°. Так как AO=BO, то треугольник ABO равнобедренный. Тогда углы при основании AB треугольника равны:
∠A=∠B=(180°-α):2=(180°-60°):2=120°:2=60°.
Значит все углы треугольника ABO равны, откуда следует, что треугольник ABO равносторонний. Отсюда
AB=AO=BO= 11 см.
Радиус r = 11 см. Применим формулу нахождения длина хорды через центральный угол и радиус:
AB=2·r·sin(α/2)=2·11 см·(1/2)=11 см.