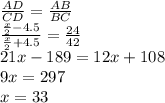Развёрткой боковой поверхности цилиндра служит прямоугольник, диагональ которого, равная 12пи, составляет с одной из сторон угол 30 градусов
диагональ боковой поверхности цилиндра d=12пи
высота цилиндра h=d*sin30=12pi*1/2=6pi <высота равна меньшей стороне развёртки
большая сторона развертки b=d*cos30=12pi*√3/2=6pi√3
большая сторона развертки b - это длина окружности ОСНОВАНИЯ b=2pi*R
радиус основания R=b/(2pi) = 6pi√3 / (2pi)=3√3
площадь основания So=pi*R^2 = pi*(3√3)^2=27pi <два основания
площадь боковой Sb=b*h=6pi√3*6pi=36pi^2√3
площадь полной поверхности цилиндра S=Sb+2So=36pi^2√3+2*27pi=36pi^2√3+54pi
ОТВЕТ
36pi^2√3+54pi
36√3pi^2+54pi
18pi (2√3pi+3)
** возможны другие варианты ответа
ответ: б) AB = 18 см, AC = 6 см в) AC = 33 см
Объяснение:
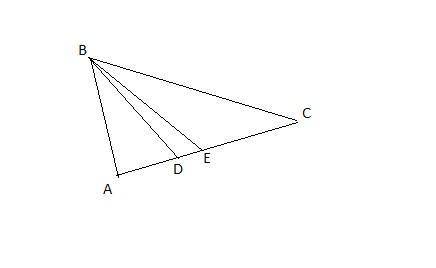
б) BC = BP + CP = 18 см
Обозначим две другие стороны Δ через x = AB и y = AC.
Из того, что периметр равен 42 получим:
x + y + 18 =42 ⇒ x + y = 24 (1)
Биссектриса делит противоположную сторону на отрезки пропорциональные сторонам ⇒
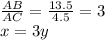
Подставим последнее равенство в (1) и получим:
4y = 24
y = 6
Тогда x = 18
в) Обозначим x = AC. Т.к. BE медиана, то AE = CE = x/2, AD = x/2 - 4.5, CD = x\2 +4.5
Биссектриса делит противоположную сторону на отрезки пропорциональные сторонам ⇒