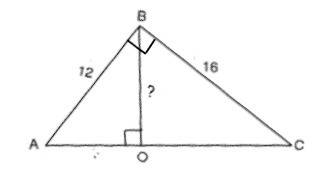
По т.Пифагора найдём гипотенузу.
АС=√(BC²+AC²)=√(256+144)=20 см
Высоту BO проще всего найти из площади треугольника.
S=BC•AB/2
S=BO•AC/2 Следовательно,
BC•AB=BO•AC, откуда
BO=BC•AB:AC
BO=16•12:20=9,6 см
-----
Вариант решения ( несколько длиннее) - его алгоритм дан ниже.
1) Находим гипотенузу по т.Пифагора
2) Катет прямоугольного треугольника – среднее пропорциональное между гипотенузой и проекцией этого катета на неё. ⇒
АВ²=АС•АО, ⇒ АО=АВ²:АС Отрезок СО находим вычитанием АО из гипотенузы или тем же что АО.
3) Высота прямоугольного треугольника, проведенная к гипотенузе, есть среднее пропорциональное между проекциями катетов на гипотенузу. ⇒
ВО²=СО•АО. Вычисления дадут ту же длину ВО=9,6 см
1)дано треугольник АВС, АВ>АС
Доказать: угол С>угла В
Решение:отложим на стороне АВ отрезок AD=AC
Так как AD<AB,то D лежии между А и В.
Следовательно угол 1 является частью угла С и, значит угол С> угла 1.
Угол 2-внешний угол треугольникa BDC, поэтому угол 2> угла B
Угол 1 и угол 2 между собой равны (треугольник ADC-равнобедренный)
Угол С> угол 1, угол 1=угол 2, угол 2>угол В следовательно угол С>угол В.
2) первый признак: если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника,то такие треугольники равны.
Второй признак: если сторона и два прилежащих к ней угла одного треугольника соответственно равны стророне и двум прилежащим к ней углам другого треугольника,то такие треугольники равны.
Третий признак: если три стороны одного треугольника соответственно равны трем сторонам другого треугольника,то такие треугольники равны.
3)пусть боковая сторона равна 5х
Тогда основание равно 2х
Так как треугольник равнобедренный то вторая боковая сторона тоже равна 5х
Отсюда P=5x+2x+5x=48
12x=48
X=4
Основание равно 2х=2×4=8
Боковая сторона 5х=5×4=20
Рисунок к 1 задаче тоже отправил если нужно будет!