1. ∠A = 90°-∠B =90°- 60° = 30°
BC = AB/2 = 5 , как катет против угла 30°
2. Прямоугольные треугольники BDC , ACB и A DC одновременно равнобедренные, что следует из условии ∠B = 45° .
AB = AD+DB = CD +CD = 2*CD =2*8 = 16
3. Допустим EC = 3
∠EBC =90°-∠BEC=90°-60° =30°⇒ EC = BE / 2 ⇔ BE =2EC = 2*3 = 6
ΔAEB - равнобедренный ( ∠ABE = ∠A ) AE = BE = 6
∠BEC =∠A + ∠ABE ⇒ ∠ABE = ∠BEC -∠A =60° -30° =30°
4. ∠DAC = 30° (следует из CD = 3,5 = 7/2 = AD/2 )
∠ D = 60° ⇒ равнобедренный ΔABC еще равносторонний
∠ B = 60°
* * * можно и по другому: В равнобедренном треугольнике BAD (AB =AD) медиана AC одновременно и биссектриса ⇒∠BAC =∠DAC и т.д.
5. ∠BPE = 180° -150°= 30° ΔPBE: BE = PE/2 ⇒PE = 2*BE =2*9 = 18
ΔBCE: CE = BE/2 =9/2 = 4,5 ; PC = PE -CE = 18 -4,5 = 13, 5
6. ∠A₁AC = (1/2)∠BAC =(1/2)*( 90° -∠B) = (1/2)*( 90° -(180° -150°) ) =30°
* * *Или из свойства внешнего угла 150° =90° +∠BAC * * *
CA₁ =AA₁/2 =20/2 = 10

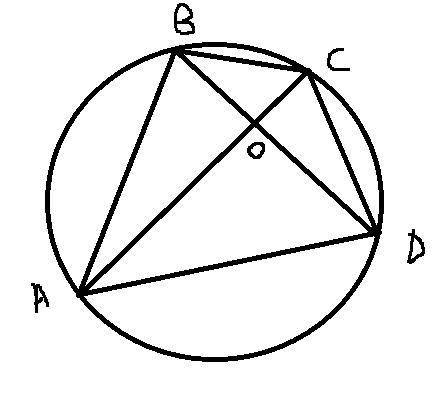
63гр
Объяснение:
Сумма углов тр-ка равна 180гр. Значит угол BDA = 180-47-74=59
угол CDB=180-106-58=16. Значит весь угол CDA=59+16=75
Сравниваем суммы противоположных углов четырехугольника (74+106=75+105) они равны и равны 180, значит вокруг этого четырехугольника можно описать окружность.
Для окружности верна теорема: Величина угла, образованного пересекающимися хордами, равна половине суммы величин дуг, заключённых между его сторонами.
В нашем случае дуга BC = 2*уголCDB = 32, а дуга AD = 2*угол ABD = 94.
Значит угол между диагоналями BOC=1/2*(BC+AD)=1/2*(32+94)=63.
1. Так как точка А - начальная точка луча, то точка С лежит между точками А и В, так как длина отрезка АВ=13, а длина отрезка АС=5 (АВ больше АС)
АВ=13
АС=5
ВС=АВ-АС
13-5=8 (см)
ответ: 8 см
2. Так как известно, АС меньше ВС на 3 см. Пусть ВС - х, тогда АС=х-3. Известно, что АС=9, значит х-3=9, х=9+3, х=12 (см) - длина отрезка ВС.
АВ=АС+ВС
9+12=21 (см)
ответ: 21 см.