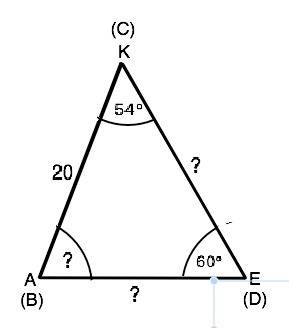
Для начала найдем неизвестные угол и стороны ∆ АКЕ. Сумма углов треугольника 180° => угол КАЕ=180°-(54°+60°=66°
По т.синусов АЕ=АК•sin54°/sin60°. KE=AK•sin66°/sin60°
sin60°=0.8660; sin54°= 0.8090; sin66°=0.9135
AE=20•0,8090/0,8660=18,683≈18,7 см; KE=20•0,9135/0,8660=21,097≈ 21,1 см
Стороны и углы треугольника ВСD имеют те же значения, что и соответствующие углы и стороны ∆ АКЕ, но в условии не указано, какие именно элементы двух треугольников равны. Если в ∆ ВСD сторона ВС=АК, и ∠D=∠Е, то ∠В=∠А=66°,∠С=∠К=54°, ВС=20 см, ВD=AE≈18,7= см, CD=KE≈21,1 см
существуют два разных размещения ковров - параллельное и перпендикулярное, при параллельном стороны длиной 10 метров параллельны, при перпендикулярном... Ну, вы сами поняли :)
при параллельном площадь перекрытой части ковров
S₁ = (a-14)(a-20) = 16 м²
(a-14)(a-20) = 16
a² - 34a + 280 = 16
a² - 34a + 264 = 0
a₁ = (34 - √(34²-4*264))/2 = (34-√100)/2 = (34-10)/2 = 24/2 = 12 м
Это хорошее решение
a₂ = (34+√100)/2 = 44/2 = 22 м
А вот это уже плохо - размер зала не даёт коврам перекрыться и по нашей формуле получается площадь прямоугольника между углами ковров. Отбрасываем.
Теперь перпендикулярное размещение.
ПЕрекрытие ковров имеет квадратную форму
S₂ = (a-17)*(a-17) = 16
(a-17)² = 16
a₃-17 = -4
a₃ = 13 м это хорошо
a₄-17 = 4
a₄ = 21 м - снова без перекрытия ковров, отбрасываем.
ответ:
Размеры зала равны 12х12 или 13х13 метров