Сначала делим четырехугольник диагональю на два треугольника.
Находим центр тяжести каждого треугольника как точку пересечения его медиан. Центр тяжести четырехугольника лежит на прямой О1О2, соединяющей центры тяжести этих треугольников.
Затем делим четырёхугольник на 2 треугольника при другой диагонали и находим так же центры тяжести других треугольников. Соединяем их отрезком О3О4.
Искомый центр тяжести четырёхугольника лежит в точке ЦТ пересечения отрезков О1О2 и О3О4.
ABD x y BCD x y
O2 3 2 O3 2 2
ADC x y ABC x y
O1 0,6667 1,3333 O4 3,3333 1,6667
ЦТ = х у
2,533 1,8667
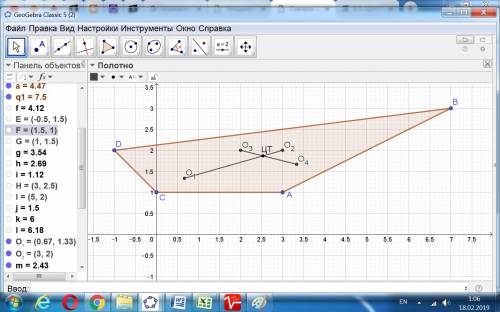
Вначале найдём уравнения сторон.
Для АВ. прямая проходит через точки А и В, ее уравнение 5х - 3у - 3 = 0
Для АС. прямая проходит через точки А и С. ее уравнение х + 3у + 3 = 0
Для ВС. прмяая проходит через точки В и С, ее уравнение 7х + 3у - 33 = 0
Медиана ВМ проходит через точку В и середину отрезка АС. Найдем координаты середины отрезка АС.
х = (6 + 0)/2 = 3 у = (-3-1)/2 = -2
Таким образом, медиана ВМ проходит через точки В(3;4) и (3;-2), и ее уравнение х = 3 (она параллельна оси ординат).
Высота BD образует прямой угол с прямой АС, уравнение которой х + 3у + 3 = 0. Условие перпендикулярности прямых - произведение их угловых коэффициентов равно -1.
АС имеет угловой коэффициент, равный - 1/3. Следовательно, угловой коэффициент искомой прямой - высоты BD - будет равен 3. Значит, уравнение высоты имеет вид:
3х - у - 5 = 0.
Найдем косинус А. Этот угол лежит между прямыми АВ = корень из 34 и АС = корень из 40. По теореме косинусов находим косинус А: он равен 2/(корень из 35)
Центр тяжести треугольника - точка пересечения его медиан. Можно отыскать, применяя дфойное интегрирование, а можно (что полегче) геометрическим
Решение 2 задачи состоит в том, что при правильном рисунке, можно сразу ответить на второй вопрос, а именно отношение площадей. BC и AD являются основанием двух запрашиваемых треугольников, а их отношение равно 5/2. Так как отношение равно 5/2, мы можем посчитать и сторону ВО = 25 * 2,5 = 62,5.