S=8√3см²
Объяснение:
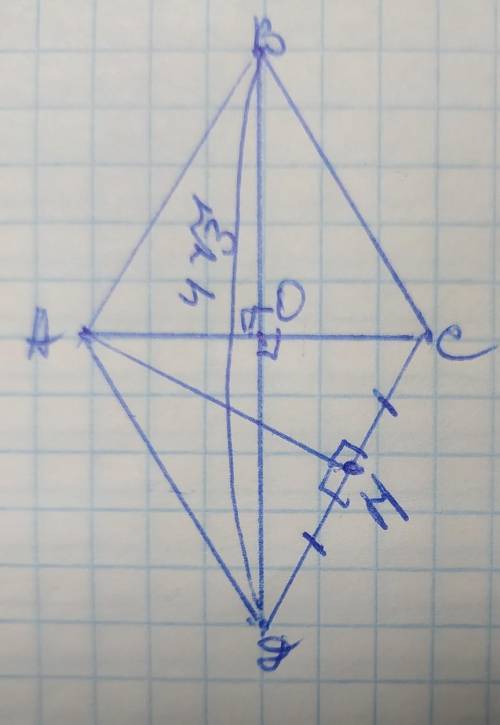
Обозначим вершины ромба АВСД, с диагоналями АС и ВД а высоту АН. Рассмотрим ∆АСД. Высота АН делит СД пополам, поэтому она является ещё медианой, следовательно ∆АСД - равнобедренный, поэтому АД=АС, а так как стороны ромба равны, то
АД=СД=АС=АВ=ВС, значит ∆АСД=∆АВС и они являются равносторонними, у которых каждый угол составляет 60°. Так как диагонали ромба, пересекаясь, образуют прямой угол и делятся пополам, то они также образуют 4 равных прямоугольных треугольника. Рассмотрим один из них: ∆АВО. В нём: ВО=ДО=4√3÷2=2√3см. Найдём сторону АВ через синус угла. Синус угла - это отношение противолежащего от угла катета к гипотенузе, тогда
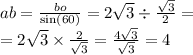
Итак: все стороны ромба и диагональ АС=4см. Поскольку нам уже известна меньшая диагональ найдём площадь ромба по формуле:
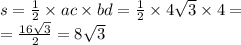
Можно использовать второй вариант, чтобы найти площадь через высоту АН, проведённую к стороне ромба.
Эта высота АН в ∆АСД равна высоте ВО в ∆АВС=2√3 (так как ∆АВС=∆АСД, и они равносторонние, то их высоты равны).
Тогда S=АД×АН=4×2√3=8√3см²